Для более детального анализа неподвижной точки для случая n = 3 необходимо знать знак выражения:
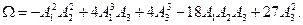
В зависимости от знака W характеристическое уравнение (8.9) имеет либо три действительных корня, либо один действительный и два комплексных сопряжённых (см. таблицу).
| Условия
| Тип корней характеристического
многочлена
| Тип неподвижной точки
|
| W < 0, А 1 > 0, А 3 < 0,
А 1 А 2 - А 3 < 0
| все корни положительны
| неустойчивый узел
|
| W < 0, А 1 > 0, А 3 > 0,
А 1 А 2 - А 3 > 0
| все корни отрицательны;
условия совпадают с условиями
асимптотической устойчивости (8.10)
| устойчивый узел
|
| W > 0, А 1 > 0, А 3 < 0,
А 1 А 2 - А 3 < 0
| действительные части корней положительны
| неустойчивый фокус
|
| W > 0, А 1 > 0, А 3 > 0,
А 1 А 2 - А 3 > 0
| действительные части корней отрицательны;
условия совпадают с условиями
асимптотической устойчивости (8.10)
| устойчивый фокус
|
| W < 0, А 1 > 0, А 3 > 0,
А 1 А 2 - А 3 < 0
| корни действительные,
но знаки их не совпадают
| седло
|
| W < 0, А 1 > 0, А 3 < 0,
А 1 А 2 - А 3 > 0
|
| W < 0, А 1 < 0, А 3 < 0
|
| W > 0, А 1 ³ 0, А 3 > 0,
А 1 А 2 - А 3 < 0
| один из корней действительный,
а два других - комплексные сопряжённые, причём знаки их действительных частей
противоположны знаку действительного корня
| седло-фокус
|
| W > 0, А 1 £ 0, А 3 > 0
|
| W > 0, А 1 > 0, А 3 < 0,
А 1 А 2 - А 3 > 0
|
 W > 0, А 1 < 0, А 3 < 0 W > 0, А 1 < 0, А 3 < 0
|
Неподвижная точка седло–фокус (см. рисунок) имеет сепаратрисную поверхность, на которой фазовые траектории расположены так же, как в окрестности фокуса на фазовой плоскости двумерных систем. Причём, для сепаратрисной плоскости состояние устойчиво, для других плоскостей - неустойчиво.

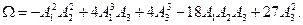
 W > 0, А 1 < 0, А 3 < 0
W > 0, А 1 < 0, А 3 < 0



