Определение. Две системы дифференциальных уравнений первого порядка называются качественно эквивалентными, если существует непрерывное взаимно однозначное преобразование, которое переводит фазовый портрет одной системы в фазовой портрет другой так, что сохраняется ориентация траекторий.
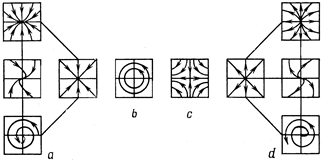
Таким образом, любая линейная система на плоскости качественно эквивалентна одной из систем, фазовые портреты которых изображены на рисунке. Десять фазовых портретов представляют типы поведения линейных систем. Следовательно, все устойчивые (неустойчивые) узлы и устойчивые (неустойчивые) фокусы эквивалентны друг другу. Это означает, что классы алгебраически эквивалентных систем можно группировать в классы качественно эквивалентных. В этом смысле для линейных систем существует только четыре типа качественного поведения: асимптотическая устойчивость (а), центр (b), седло (c) и неустойчивость (d).