Примеры анализа систем с использованием первого метода Ляпунова
3.1. Анализ реакционной схемы Рассмотрим проточный реактор идеального смешения, в котором протекают реакции по схеме:
Математическая модель реактора имеет вид:
Определим стационарное состояние в реакторе и тип этого состояния. Неподвижную точку находим из условия:
Запишем характеристическое уравнение для модели реактора и определим его корни:
при при Таким образом, если константа автокаталитической реакции больше 3.2. Анализ модели процесса кристаллизации Рассмотрим процесс кристаллизации в реакторе, в котором с постоянной скоростью b происходит отбор зародышей и с постоянной скоростью bd происходит пополнение крупными частицами. Пусть в реакторе происходит растворение мелких частиц и кристаллизация крупных, а также пусть зародышеобразование происходит по вторичному механизму. Математическая модель такой системы имеет вид:
где m0 - нулевой момент функции распределения кристаллов по размерам, характеризующий общее количество частиц в единице объёма реактора; m1 - первый момент функции распределения, характеризующий суммарный линейный размер кристаллов; k - константа скорости образования зародышей; k m1 - скорость образования зародышей; b - скорость отбора зародышей; bd - скорость пополнения крупными частицами; h1 - скорость роста кристаллов; h2 - скорость растворения кристаллов; db - суммарный линейный размер поступающих частиц. Средний размер кристалла в кристаллизаторе определяется соотношением:
Нас интересует, как будет вести себя средний размер кристалла с течением времени. Определим стационарное состояние в реакторе:
Очевидно, что стационарное состояние существует только при выполнении условий:
Получим характеристическое уравнение:
Определим его корни:
Как видно, корни чисто мнимые, т.е. стационарное состояние является центром. Следовательно, в такой системе размер кристалла будет колебаться вокруг среднего значения с постоянными периодом и амплитудой в течение длительного времени.
4. Определение типа неподвижных точек для систем n -го порядка Рассмотрим систему обыкновенных дифференциальных уравнений n -го порядка. В качественной теории дифференциальных уравнений формулируются следующие теоремы: Теорема 1. Если все корни характеристического уравнения системы Теорема 2. Если хотя бы один корень характеристического уравнения системы имеет положительную действительную часть, то неподвижная точка неустойчива по Ляпунову; Теорема 3. Если характеристическое уравнение системы имеет простые корни с нулевой действительной частью или простые чисто мнимые корни, либо простой нулевой корень и простые чисто мнимые корни, а все остальные корни (если они имеются) имеют отрицательные действительные части, то неподвижная точка устойчива по Ляпунову (нейтральная устойчивость). Легко видеть, что рассмотренные ранее возможности поведения корней характеристического уравнения для случая n = 2 являются частным случаем данных теорем.
5. Необходимый признак асимптотической устойчивости линейных систем (критерий Раусса-Гурвица) Характеристическое уравнение
Из коэффициентов характеристического уравнения (8.8) составим матрицу, называемую матрицей Раусса-Гурвица:
Для того чтобы все корни характеристического многочлена (8.8) имели строго отрицательные действительные части, необходимо и достаточно, чтобы все главные диагональные миноры матрицы Раусса-Гурвица, составленной из коэффициентов характеристического многочлена, были строго положительны:
Критерий Раусса-Гурвица является критерием асимптотической устойчивости для линейных систем. Рассмотрим случай n = 2. Для многочлена (8.7) построим матрицу Раусса-Гурвица:
Критерий Раусса-Гурвица определяет условия
соответствующие устойчивому фокусу или устойчивому узлу (см. таблицу, приведённую в разделе "Классификация неподвижных точек на плоскости";). Рассмотрим случай n = 3. Характеристический многочлен имеет вид:
Запишем матрицу Раусса-Гурвица
Тогда условия критерия асимптотической устойчивости выглядят следующим образом:
или
|

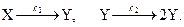
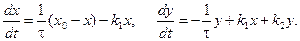
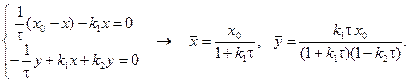
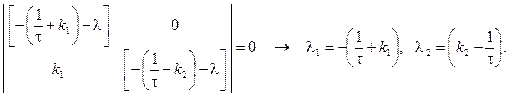
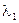 всегда отрицательно; знак
всегда отрицательно; знак 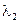 зависит от соотношения времени пребывания и константы автокаталитической реакции следующим образом:
зависит от соотношения времени пребывания и константы автокаталитической реакции следующим образом: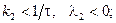
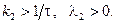
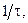 стационарное состояние является седлом и неустойчиво, если меньше - стационарное состояние является устойчивым узлом. Отметим, что неустойчивость реакций такого типа предсказывает метод функций Ляпунова (избыточного производства энтропии). Причина неустойчивости кроется в наличии обратной автокаталитической связи. Действительно, если увеличить рабочий объём реактора так, чтобы
стационарное состояние является седлом и неустойчиво, если меньше - стационарное состояние является устойчивым узлом. Отметим, что неустойчивость реакций такого типа предсказывает метод функций Ляпунова (избыточного производства энтропии). Причина неустойчивости кроется в наличии обратной автокаталитической связи. Действительно, если увеличить рабочий объём реактора так, чтобы 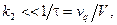 то произойдет гашение возникающих флуктуаций; если же
то произойдет гашение возникающих флуктуаций; если же 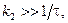 флуктуации не затухают, и стационарный режим будет неустойчивым.
флуктуации не затухают, и стационарный режим будет неустойчивым.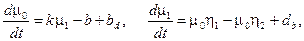
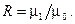
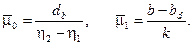

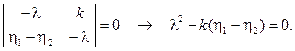
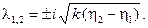
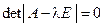 имеют отрицательные действительные части, то неподвижная точка асимптотически устойчива;
имеют отрицательные действительные части, то неподвижная точка асимптотически устойчива;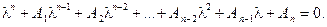 (8.8)
(8.8)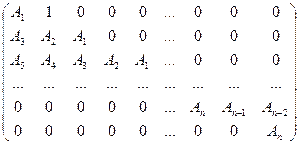
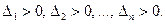
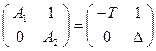
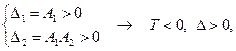
 (8.9)
(8.9)
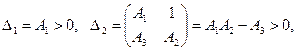
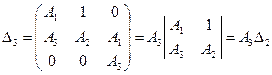
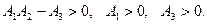 (8.10)
(8.10)


