Первый метод Ляпунова
План лекции Методы исследования линейных систем 1. Первый метод Ляпунова 2. Классификация неподвижных точек на плоскости 3. Примеры анализа систем с использованием первого метода Ляпунова 3.1. Анализ реакционной схемы 3.2. Анализ модели процесса кристаллизации 4. Определение типа неподвижных точек для систем n -го порядка 5. Необходимый признак асимптотической устойчивости линейных систем (критерий Раусса-Гурвица) 6. Детальный анализ типа неподвижной точки для системы 3-го порядка 7. Пример анализа реакционной схемы с использованием критерия Раусса-Гурвица 8. Качественная эквивалентность систем
Первый метод Ляпунова Как определить, не решая систему уравнений, тип неподвижной точки и устойчива ли она? Для этого используют первый метод Ляпунова для определения типа устойчивости неподвижной точки. Рассмотрим систему уравнений:
Решение системы уравнений (8.1) представим в виде:
Подставим (8.2) в исходную систему уравнений (8.1) и получим:
или после сокращения
В матричной форме запись уравнений (8.3) выглядит следующим образом: (A - l Е) С = 0. (8.4) Для того чтобы система (8.4) имела нетривиальные решения С ¹ 0, необходимо, чтобы
т. е.
Собственные числа l i матрицы А определяют из условия (8.5). Раскрывая детерминант, получим квадратичное уравнение относительно l, называемое характеристическим:
Следовательно, исходная система (8.1) допускает решения:
По значению собственных чисел матрицы А можно определить тип точки и тип её устойчивости. Существуют три возможности поведения собственных чисел, соответствующих трём видам устойчивости неподвижных точек: 1) если l1, l2 имеют действительные отрицательные части, то неподвижная точка асимптотически устойчива; 2) если хотя бы один из корней l i имеет положительную действительную часть, то неподвижная точка неустойчива; 3) если корни чисто мнимые или один из корней имеет нулевую действительную часть, а действительная часть другого – отрицательна, то неподвижная точка нейтрально устойчива.
|

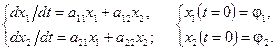 (8.1)
(8.1)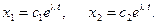 (8.2)
(8.2)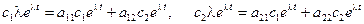
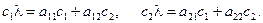 (8.3)
(8.3)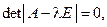
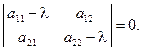 (8.5)
(8.5)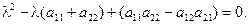 (8.6)
(8.6)