Классификация неподвижных точек на плоскости
Для определения типа неподвижной точки рассмотрим уравнение (8.6) более подробно. Введём обозначения:
Тогда квадратичное уравнение (8.6) примет вид
и будет иметь корни
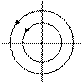
Анализ корней уравнения (8.7) позволяет классифицировать неподвижные точки в зависимости от значений коэффициентов матрицы А, не прибегая к решению системы уравнений. Классификация неподвижных точек представлена в таблице.
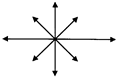
Следовательно, если корни характеристического уравнения (8.7): а) действительные и одного знака, то неподвижная точка – узел, причём
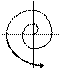
б) действительные и различных знаков, то неподвижная точка - седло; в) комплексно-сопряженные, то неподвижная точка - фокус, причём
г) чисто мнимые, то неподвижная точка - центр.
|

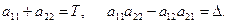
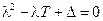 (8.7)
(8.7)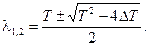
 D > 0, Т > 0 -
неустойчивый узел
D > 0, Т > 0 -
неустойчивый узел
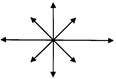
 D > 0, Т < 0 - устойчивый узел
D > 0, Т < 0 - устойчивый узел


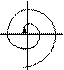 D < 0 - седло
D < 0 - седло
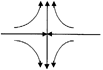
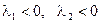 - устойчивый узел,
- устойчивый узел,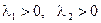 - неустойчивый узел;
- неустойчивый узел;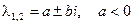 - устойчивый фокус,
- устойчивый фокус,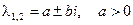 - неустойчивый фокус;
- неустойчивый фокус;


