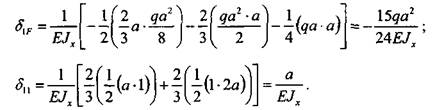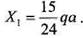Решение. Для решения этой задачи воспользуемся методом сил
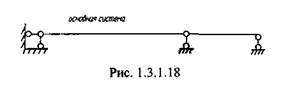
Для решения этой задачи воспользуемся методом сил. В качестве основной системы выберем ту же балку, но с размещенным в точке В виртуальным шарниром (рис. 1.3.1.18). Тогда в качестве эквивалентной будет выступать основная система, к которой помимо внешней нагрузки приложены два одинаковых неизвестных си-
ловых фактора X, (два неизвестных момента). Величина Хх должна удовлетворять следующему условию: угол поворота точки В равен нулю, т. к. на самом деле шарнир в этой точке отсутствует.
Составим каноническое уравнение метода сил (2.6.37):
где
Из канонического уравнения определим X.: 36 Глава 1.Сопротивление материалов Дня того чтобы определить коэффициенты канонического уравнения, воспользуемся интегралом Мора, а именно:
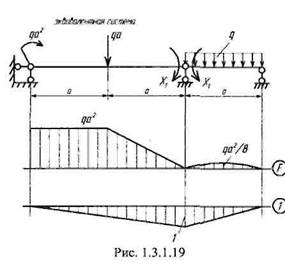
Здесь сто неизвестного фактора мент от внешней нагрузки (эпюра / на рис. 1.3.1.19). Разобьем всю балку на три равных участка длиной а и свяжем с началом каждого участка локальную систему координат, в которой будут выполняться все дальнейшие расчеты. Подставляя аналитические выражения и вычисляя интегралы, получим:
При расчете более сложных моделей балочных и рамных конструкций метод Мора является слишком трудоемким, так как требует составления аналитического выражения подынтегральных функций. Для упрощения вычислений используют метод Верещагина [5], суть которого заключается в следующем. Пусть на участке длиной / нужно взять интеграл от произведения двух функций
станты. Тогда интеграл можно заменить следующим выражением:
где
координатой центра тяжести первой эпюры. Если линейными являются обе функции, то операция перемножения обладает свойством коммутативности, т. е. не имеет значения, умножается ли площадь первой эпюры на ординату второй или площадь второй эпюры на ординату первой. 1.3. Изгиб __________________________________________________________________ 37 Определим теперь методом Верещагина коэффициенты канонического уравнения. Коэффициент
Как видно, оба рассмотренных метода — Мора и Верещагина — дают одинаковые результаты.
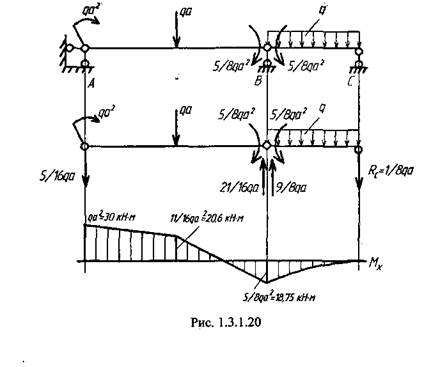
Тогда эквивалентную систему приобретает вид (рис. 1.3.1.20). Рассматривая части балки, расположенные справа и слева от шарнира, как самостоятельные независимые системы, с помощью уравнений статики найдем реакции в опорах. После этого строим эпюру изгибающих моментов.
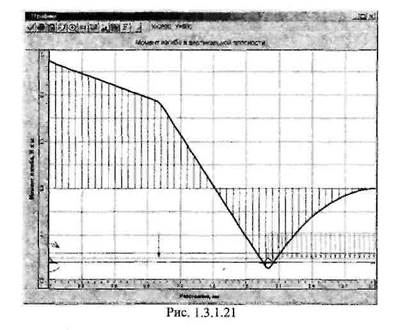
38 Глава 1.Сопротивление материалов Решение этой задачи, выполненное с помощью модуля АРМ Beam, представлено на рис. 1.3.1.21.
1.3.2. Расчет плоских рамных конструкций Задача 1. Для плоской рамы, изображенной на рис. 1.3.2.1, построить эпюры внутренних силовых факторов.
|

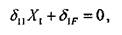
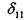 — поворот точки В в направлении неизвестного силового фактора под действием единичного момента, приложенного вместо
— поворот точки В в направлении неизвестного силового фактора под действием единичного момента, приложенного вместо 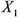 ;
; 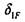 — поворот точки В в направлении неизвестного момента под действием внешней нагрузки.
— поворот точки В в направлении неизвестного момента под действием внешней нагрузки.
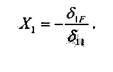
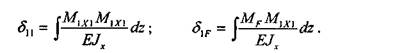
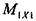 — изгибающий момент от единичной нагрузки, приложенной вме-
— изгибающий момент от единичной нагрузки, приложенной вме-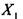 (эпюра ^на рис. 1.3.1.1 Я);
(эпюра ^на рис. 1.3.1.1 Я); 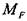 — изгибающий мо-
— изгибающий мо-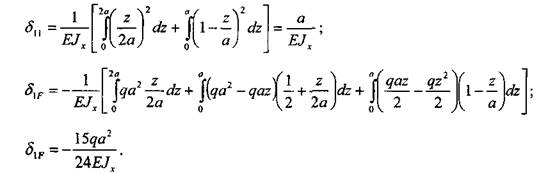
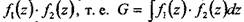 , при условии, что по крайней мере одна из этих функций — линейная, например,
, при условии, что по крайней мере одна из этих функций — линейная, например, 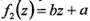 , где а и b— некоторые кон-
, где а и b— некоторые кон-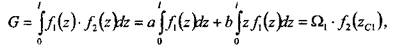
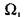 — площадь, ограниченная кривой, т. е. площадь эпюры
— площадь, ограниченная кривой, т. е. площадь эпюры 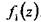 , а
, а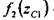 — значение линейной функции
— значение линейной функции 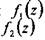 в точке
в точке 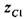 , которая является
, которая является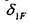 найдем перемножением эпюры F на эпюру /, а коэффициент
найдем перемножением эпюры F на эпюру /, а коэффициент 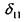 — умножением эпюры / саму на себя:
— умножением эпюры / саму на себя: