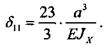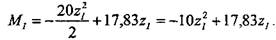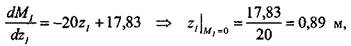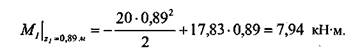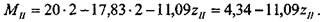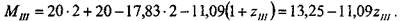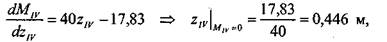Индекс стержня 1

 

 

Узел конца	Сила [Н]	Момент [Н*м]
Fx (осевая)	Fy	Fz	Мх (круче­ния)	My	Mz
	-20000.00	0.00	-40000.00	0.00	-20000.00	0.00
	-20000.00	0.00	0.00	0.00	-0.00	0.00

1.3. Изгиб 43

Индекс стержня 2

 

 

Узел конца	Сила [Н]	Момент [Н*м]
Fx (осевая)	Fy	Fz	Мх (круче­ния)	My	Mz
	40000.00	20000.00	-0.00	0.00	0.00	40000.00
	40000.00	20000.00	-0.00	-0.00	0.00	20000.00

Индекс стержня 3

 

Узел конца		Сила [Н]		Момент [Н*м]
Fx (осевая)	Fy	Fz	Мх (круче­ния)	My	Mz
	40000.00	20000.00	-0.00	-0.00	0.00	40000.00
	40000,00	20000.00	-0.00	-0.00	0.00	20000.00

Реакции в опоре

 

 

N	Узел		Сила [Н]	Момент [Н*м]
X	У		X	У	Z
		0.0000	0.0000	—20000.0000	-О.0000	П 00.0000	0.0000
		-0.0000	-0.0000	20000.0000	0.0000	0.0000	-0.0000

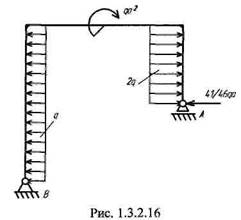
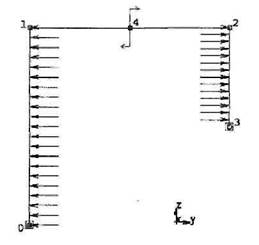
Задача 2. Для плоской статически неопределимой рамы (рис. 1.3.2.11)построить эпюру изгибающих моментов, если q = 20 кН/м, а = 1 м.

44 Глава 1.Сопротивление материалов

Решение

В качестве основной выберем систему, изображенную на рис. 1.3.2.12. Как вид­но из этого рисунка, опора А получила возможность горизонтального перемеще­ния. Для того чтобы основная система была эквивалентной исходной, нужно найти величину неизвестного силового фактора Х_х. Его значение должно быть таким, чтобы перемещение по направлению Х_х равнялось нулю. Каноническое уравнение метода сил будет иметь следующий вид:

 

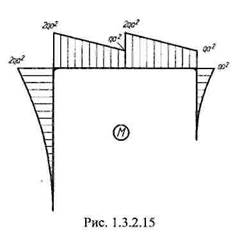
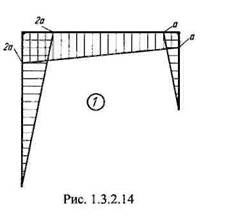
Нагрузим основную систему сначала только заданной внешней нагрузкой, а по­том только единичной силой,приложенной вместо неизвестной реактивной силы Х_х (рис. 1.3.2.13). Построим эпюры изгибающих моментов от единичного фактора (рис. 1.3.2.14) и от внешней нагрузки (рис.1.3.2.15).

 

1.3. Изгиб 45

Коэффициенты канонического уравнения находим методом перемножения эпюр. Умножая единичной эпюры саму на себя, получим коэффициент ,

 

Перемножив эпюру внешней нагрузки и единичную эпюру, найдем

 

 

1.3.2.16.

а эквивалентная система принимает вид, показанный на рис.

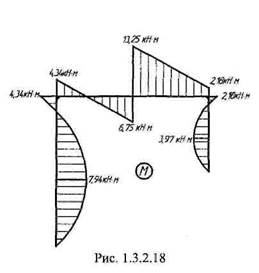
Затем определим реакции в шарнирах (рис. 1.3.2.17) и построим эпюру изги­бающих моментов (рис. 1.3.2.18).

Эпюра моментов строится аналогично предыдущей задаче: рама разбивается на ряд участков (рис. 1.3.2.3— рис. 1.3.2.6), затем для каждого участка с помощью уравнения равновесия записывается аналитическое выражение функции изгибаю­щих моментов.

Определяем положение точки экстремума:

Для участка / (начало отсчета координаты z, —как на рис. 1.3.2.3):

46 Глава 1.Сопротивление материалов

 

Для участка II (начало отсчета координаты z„ — как на рис. 1.3.2.4):

Для участка III (начало отсчета координаты z,„ —как на рис. 1.3.2.5):

Положение точки экстремума:

Для участка IV (начало отсчета координаты z_IV —как на рис. 1.3.2.6):

Ниже приведены результаты расчета данной задачи в модуле АРМ Struc-ture3D. Результаты содержат: вид спереди (ось х направлена на нас), информацию по стержням и приложенным к раме нагрузкам, значения внутрен­них силовых факторов в узлах конструкции и реакции в опорах. Также показаны диаграммы моментов изгиба в координатных плоскостях XZ и XY (примени-

1.3. Изгиб 47

тельно к локальной системе координат каждого из стержней), причем на диа­грамме моментов изгиба в плоскости XY показаны все внешние нагрузки, а на диаграмме моментов изгиба в плоскости XZ - только момент изгиба.

Результаты расчета в АРМ Structure3D: Название вида: Вид спереди
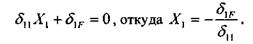
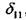