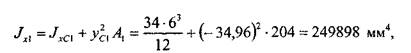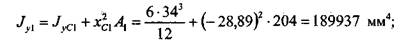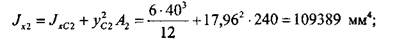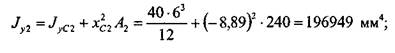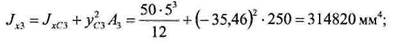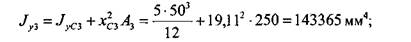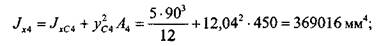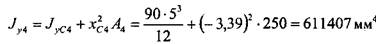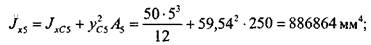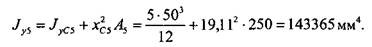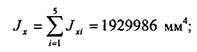РАСЧЕТ ГЕОМЕТРИЧЕСКИХ ХАРАКТЕРИСТИК СЕЧЕНИЯ
Задача 1. Для заданного сечения, изображенного на рис. 1.4.1, определить моменты инерции относительно центральных осей.
Решение Сначала необходимо найти положение центра тяжести заданной фигуры. Для этого выберем две произвольные декартовые оси, xt и у1г и определим статические моменты инерции сечения относительно этих осей. Оси следует выбирать таким образом, чтобы относительно них можно было определить статические моменты и моменты инерции наиболее простым способом. Для удобства проведения расчетов разобьем данное сечение на прямоугольники, геометрические характеристики которых легко находятся (рис. 1.4.2), и вычислим площадь каждого прямоугольника, а затем и площадь всей фигуры в целом:
Статические моменты прямоугольных фигур относительно выбранных осей (2.3.1):
1.4. Расчет геометрических характеристик сечения 61
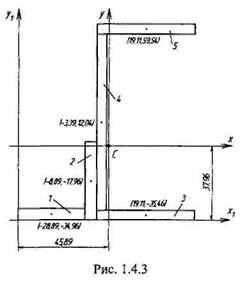
= 3-204 + 20-240 + 2,5-250 + 50-450+97,5-250 = 52912мм3. По формуле 2.3.3 определим положение центра тяжести (рис. 1.4.3):
Далее нужно вычислить моменты инерции каждого из прямоугольников относительно осей, проходящих через центр тяжести сечения. Это можно сделать, используя теорему о параллельном переносе осей (2.3.12):
где собственных центральных осей (2.3.8), а
Моменты инерции всей фигуры получаем суммированием моментов инерции ее составляющих:
Эти вычисления можно выполнить, используя модуль АРМ Beam системы АРМ WinMachine. С его помощью можно рассчитать геометрические характеристики сечений любой сложности. Для этого необходимо изобразить произвольную балку и задать для нее требуемое поперечное сечение. Для задания сечения можно ис- 1.4. Расчет геометрических характеристик сечения 63
|


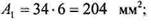
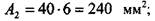
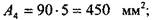
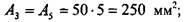
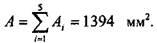
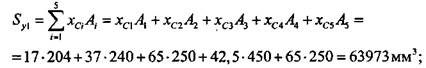
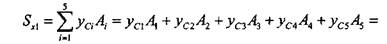
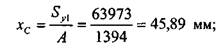
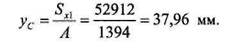

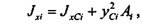
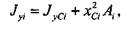
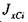 и
и 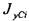 — моменты инерции каждого из прямоугольников относительно
— моменты инерции каждого из прямоугольников относительно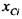 и
и 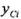 — координаты положения центров масс прямоугольников в координатной плоскости х, у. Имеем:
— координаты положения центров масс прямоугольников в координатной плоскости х, у. Имеем: