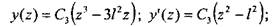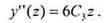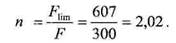Решение
Для того чтобы решить эту задачу, воспользуемся энергетическим методом определения критической силы (2.9.14), согласно которому
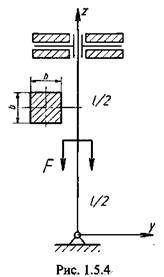
Здесь U — потенциальная энергия изгиба стержня, а Для определения функции прогиба стержня в виде полинома, старшая степень которого равна числу граничных условий. Граничные условия для данной задачи запишутся следующим образом: 70 Глава 1. Сопротивление материалов
Следовательно, функция прогиба будет иметь вид Используя граничные условия, найдем коэффициенты полинома:
В окончательном виде для функции прогиба и ее производных имеем: Как видно, во всех выражениях присутствует неизвестная константа С3. В рассматриваемом случае она не играет никакой роли, так как в дальнейшем, при вычислении критической силы, просто сократится. Получим:
Коэффициент запаса устойчивости:
На рис. 1.5.5 показано окно результатов расчета данного стержня на устойчивость в программе АРМ Structure3D. Расчетная модель строится с учетом рекомендаций, указанных в предыдущей задаче.
|
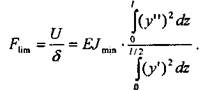
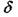— величина вертикального перемещения точки приложения силы F.
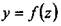представим эту функцию
