Статический момент
инерции двутавра относительно вспомогательной оси х,;
статический момент инер- ции швеллера относительно вспомогательной оси х{. Для координаты ус центра масс сечения имеем
66 Глава 1. Сопротивление материалов
Тогда в принятых на рис. 1.4.8 обозначениях получаем: Теперь с помощью теоремы об изменении момента инерции при параллельном переносе осей определяем моменты инерции швеллера и двутавра относительно
центральных осей сечения (рис. 1.4.8): На рис. 1.4.9 представлены результаты расчета заданного сечения, полученные, аналогично предыдущей задаче, с помощью программного модуля АРМ Beam. Создание сечения в АРМ Beam происходит следующим образом: вначале средствами графического редактора АРМ Graph изображается профиль сечения (при этом стан-
дартные составляющие сечения импортируются из встроенной в редактор АРМ Graph базы данных стандартных элементов), а затем файл с изображенным сечением сохраняется с расширением dxf. Сохраненный таким образом файл в дальнейшем можно импортировать во встроенный в программу АРМ Beam редактор сечений. 1.5. РАСЧЕТ УСТОЙЧИВОСТИ СЖАТЫХ СТЕРЖНЕЙ Задача 1. Найти критическую силу крепления стержня длиной / = 2 м, если Е = 2 • 105 Н/мм2.
Решение Под устойчивостью понимается свойство механической системы сохранять свое состояние при внешних воздействиях. Находясь в состоянии устойчивости, механическая система при приложении любого сколь угодно малого внешнего воздействия возвращается в исходное положение после снятия этого воздействия. Значение внешней силы, при которой система переходит из устойчивого в неустойчивое состояние, называется критической силой. Для того чтобы найти значение критической силы равновесие механической системы, в данном случае — сжатого двухопорного стержня, нагруженного осевой силой F. Прежде всего отбросим одну из опор и заменим ее действие реакцией (рис. 1.5.2). Дифференциальное уравнение изгиба стержня, справедливое при малых прогибах, имеет следующий вид (2.9.1):
где Jmin — минимальный осевой момент инерции (2.3.4); М = —Fy + Rz — изгибающий момент в сечении с координатой z.
68 Глава 1. Сопротивление материалов Уравнение изгиба стержня можно представить в форме
Общее решение этого уравнения, как известно, следует искать в виде
Постоянные интегрирования d и С2 можно найти, используя граничные условия:
Из первого граничного условия находим С|=Ю. Второе граничное условие эквивалентно однородной системе линейных алгебраических уравнений с двумя неизвестными, С2 и R,
Эта система будет иметь ненулевое решение при нулевом определителе:
Раскрывая определитель, получим трансцендетное уравнение
Тогда
Для заданного сечения
1.5. Устойчивость сжатых стержней 69 Возможности программы АРМ Structure3D позволяют рассчитать систему на устойчивость и в качестве результата получить коэффициент запаса устойчивости при заданном загружении. Необходимо заметить, что создание стержневой модели в АРМ Structure3D имеет одну особенность. Для получения верного результата стержень следует разбить как минимум на два участка, т. е. создать хотя бы один дополнительный узел. Это связано с необходимостью обеспечения достаточного числа степеней свободы в месте максимального прогиба балки (при расчете подобных конструкций методом конечных элементов необходимо наличие узлов, которые могли бы свободно перемещаться, [4]).
Окно с результатами расчета стержня, нагруженного силой F = 1 кН, показано на рис. 1.5.3. Для того чтобы получить значение критической силы, нужно умножить величину нагрузки на коэффициент запаса устойчивости:
Задача 2. Рассчитать на устойчивость стержень, изображенный на рис. 1.5.4, если F = 200 кН;
|



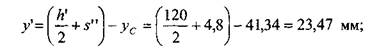






 при указанных на рис. 1.5.1 условиях за-
при указанных на рис. 1.5.1 условиях за-
 необходимо рассмотреть
необходимо рассмотреть





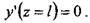



 имеющее бесконечное множество решений. Решая это уравнение графически, найдем его первый корень:
имеющее бесконечное множество решений. Решая это уравнение графически, найдем его первый корень: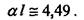
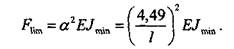




 =3 м;
=3 м;  = 2105МПа;
= 2105МПа; 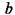 =101 мм;
=101 мм; 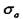 =160 МПа.
=160 МПа.


