Решение. Так как заданная конструкция кососимметрична, то основную систему удобно представить в виде, изображенном на рис
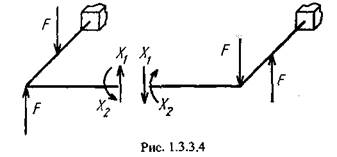
Так как заданная конструкция кососимметрична, то основную систему удобно представить в виде, изображенном на рис. 1.3.3.4, т. е. «разрезать» исходную раму по плоскости симметрии. Тогда в сечении будут возникать только кососимметрич-ные факторы, следовательно, число канонических уравнений сократится. Кроме того, поскольку эпюра моментов для всей балки в целом также будет кососимметрична, то можно строить эпюру только для одной половины балки.
Таким образом, исходная задача свелась к нахождению двух неизвестных силовых факторов из условия равенства нулю перемещение и угла поворота в разрезанном сечении (рис. 1.3.3.5). Составим систему канонических уравнений метода сил:
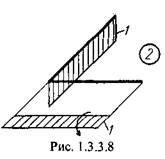
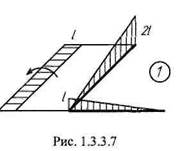
Построим эпюры отдельно от внешней нагрузки (рис. 1.3.3.6) и от единичных факторов, замещающих Хх (рис. 1.3.3.7) и Х2 (рис. 1.3.3.8), а затем найдем коэффициенты системы канонических уравнений. В итоге получим следующую систему уравнений: 1.3. Изгиб 57
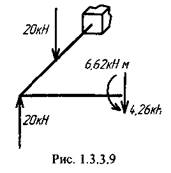
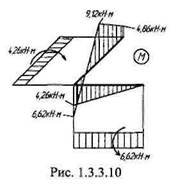
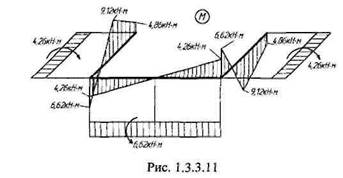
Тогда эквивалентную систему можно представить в виде, показанном на рис. 1.3.3.9, и построить эпюру изгибающих и крутящих моментов для левой части стержня (рис. 1.3.3.10). Эпюру для правой части стержня, учитывая симметрию задачи, получим зеркальным отображением эпюры правой части. Окончательный вид эпюры для всего стержня приведен на рис. 1.3.3.11. Ниже представлены результаты расчета этой задачи в программе АРМ Structure3D: диаграммы моментов изгиба и моментов кручения (цифрами показаны номера узлов конструкции), информация по стержням, приложенным нагрузкам, значения внутренних силовых факторов в узлах и реакции в опорах.
58 Глава 1.Сопротивление материалов Результаты расчета в АРМ Structure3D: Количество стержней 5
|