Длянахождения статического момента выделяем на поверхности площадки
контакта находящийся на расстоянии
(рис. 2.1.2.3) и вычисляем S. по формуле Приложенную к соединению внешнюю силу F представим в виде совокупности проекций на вертикальную (индекс
Условие нераскрытия стыка. Запишем условие нераскрытия стыка (4.1.48): где
том; 2.1. Резьбовые соединения 85
фигуры, находящейся в контакте, относительно оси у;
z = 5 — количество винтов. Определим осевой момент сопротивления Wy фигуры, совпадающей с плоскостью контакта. Первым этапом здесь является процедура нахождения осевого момента инерции. С целью определения момента инерции, как и в случае расчета статического момента, выделяем элементарную площадку (рис. 2.1.2.3) площадью
Момент инерции относительно оси у, проходящей через центр тяжести стыка, вычисляем по известным правилам параллельного переноса осей: 86 Глава 2. Соединения элементов машин Окончательную величину силы затяжки
Сила, действующая наиболее нагруженный винт. Найдем силу, действующую на наиболее нагруженный элемент крепления. Дня этого сначала разобьем все винты на группы, в зависимости от их удаленности от оси у (в каждую группу будут входить винты с одинаковыми координатами х). В данной задаче есть три таких группы (рис. 2.1.2.4). Вычислим координаты этих групп
Сила, действующая на каждый из винтов, складывается из трех составляющих: силы затяжки F0, силы от внешней отрывающей нагрузки
Для того чтобы рассчитать силу от момента, действующую на наиболее нагруженный винт, предположим, что эта сила линейно зависит от местоположения винта, т. е. от расстояния до оси у, откуда следует, что
При этом предположении уравнение равновесия для всего стыка, находящегося под действием одного только опрокидывающего момента, имеет вид
или
Очевидно, что самым нагруженным будет винт третьей группы (в третьей группе находится всего один винт), т. к., во-первых, эта группа наиболее удалена от 2.1. Резьбовые соединения 87 центра тяжести стыка, а во-вторых, сила, действующая на винты этой группы, противоположна силе затяжки. Тогда
В итоге получаем силу, действующую на максимально нагруженный винт (4.1.57):
где усилие затяжки увеличено на коэффициент, учитывающий наличие напряжений сдвига от момента трения в резьбе. Определение геометрических размеров винта из условия прочности. Зная приходящуюся на винт максимальную силу, можно определить его размеры из условия прочности на растяжение (4.1.12):
где Дня заданного класса прочности предел прочности материала винта тролируемым, тогда коэффициент запаса статической прочности можно положить равным п = 3. Величину допускаемого напряжения винта при растяжении вычисляем по формуле 4.1.17,
Следовательно, заданным условиям удовлетворяет винт М12, размеры которого:
Расчет момента завинчивания. Момент завинчивания (4.1.8):
88 Глава 2. Соединения элементов машин
где циент трения. рад — приведенный коэффи-
Проверка условия несдвигаемости. Проверим условие несдвигаемости (4.1.61 Видно, что условие несдвигаемости не выполняется, следовательно, в направлении действия горизонтальной силы нужно поставить упор, который воспримет нагрузку от сдвига. Расчет соединения в модуле АРМ Joint Расчет проводится аналогично предыдущей задаче: соединение нагружается только внешней вертикальной силой и моментом, создаваемым горизонтальной силой. Необходимые значения различных коэффициентов задаются в полях вво-
да диалогового окна «Постоянные параметры». Результаты вычислений и карта давлений с нагрузками на каждый из винтов приводятся на рис. 2.1.2.5, 2.1.2.6.
|

 элементарный участок кольца площадью
элементарный участок кольца площадью



 ) и горизонтальную (индекс h) оси, а затем по правилам механики перенесем эти проекции в центр тяжести стыка. Поскольку все внешние силовые факторы перенесены в центр тяжести стыка, то система внешнего нагружения может быть сведена к действию силы
) и горизонтальную (индекс h) оси, а затем по правилам механики перенесем эти проекции в центр тяжести стыка. Поскольку все внешние силовые факторы перенесены в центр тяжести стыка, то система внешнего нагружения может быть сведена к действию силы  и момента изгиба (опрокидывающего момента)
и момента изгиба (опрокидывающего момента) 





 — давление от силы затяжки
— давление от силы затяжки 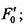
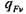 и
и  — давления, вызванные соответственно отрывающей силой и момен-
— давления, вызванные соответственно отрывающей силой и момен- — осевой момент сопротивления и момент инерции площади
— осевой момент сопротивления и момент инерции площади — расстояние от центральной оси до наиболее удаленной точки поверхности касания, в данном случае
— расстояние от центральной оси до наиболее удаленной точки поверхности касания, в данном случае  =
= 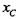 =112,2 мм;
=112,2 мм; — коэффициент основной нагрузки, значения которого для контакта металлических поверхностей лежат в диапазоне
— коэффициент основной нагрузки, значения которого для контакта металлических поверхностей лежат в диапазоне  , так что можно принять
, так что можно принять  = 0,25;
= 0,25;

 . Тогда, исходя из определения (2.3.4), для момента инерции относительно оси у' запишем:
. Тогда, исходя из определения (2.3.4), для момента инерции относительно оси у' запишем: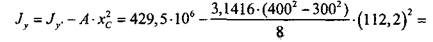




 находим с учетом коэффициента запаса на нераскрытие
находим с учетом коэффициента запаса на нераскрытие 

 = 1,2,3:
= 1,2,3: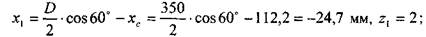


 и силы от момента
и силы от момента Сила затяжки уже известна, найдем силу от вертикальной нагрузки:
Сила затяжки уже известна, найдем силу от вертикальной нагрузки:





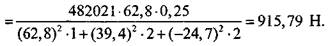


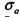 — допускаемое напряжение растяжения винта; dx — внутренний диаметр резьбы.
— допускаемое напряжение растяжения винта; dx — внутренний диаметр резьбы. = 400 МПа, а предел текучести
= 400 МПа, а предел текучести  Примем усилие затяжки некон-
Примем усилие затяжки некон- МПа, а внутренний диаметр резьбы — из условия прочности (4.1.12):
МПа, а внутренний диаметр резьбы — из условия прочности (4.1.12):





 = 1,5 — коэффициент запаса по сдвигу,
= 1,5 — коэффициент запаса по сдвигу,







