СОЕДИНЕНИЯ ДЕТАЛЕЙ ВРАЩЕНИЯ 2.2.1. Расчет соединения с натягом
Подобрать посадку, обеспечивающую соединение червячного колеса с валом (рис. 2.2.1.1). Нагрузки, действующие на соединение от зацепления: передаваемый момент вращения
Диаметр соединения d = 50 мм; условный наружный диаметр ступицы d2 = 65 мм; длина посадочной поверхности / = 100 мм. Шероховатость вала и отверстия
Вал выполнен из стали 45 (предел прочности
Расчет В данной задаче рассматривается случай общего нагружения соединения вращения, когда среди приложенных внешних нагрузок имеются следующие силовые факторы: • момент вращения; • осевая сила; • радиальная сила; • момент изгиба (опрокидывающий момент). 98 Глава 2. Соединения элементов машин Натяг в таких соединениях достигается посредством разности посадочных размеров вала и сопряженного с ним отверстия. Так как момент вращения и осевая сила могут вызвать сдвиг поверхности одной детали относительно другой, а действие момента изгиба и радиальной силы может привести к появлению зазора между деталями, то соединение с натягом следует рассчитывать по двум критериям: критерию несдвигаемости соединения и критерию нераскрытия стыка. Вначале определяется минимально необходимое давление в стыке, при котором выполняются оба условия, несдвигаемости и нераскрытия. Далее по наибольшему из найденных давлений определяется минимально требуемый натяг, после чего подбирается посадка, которая может обеспечить этот натяг. Определение минимально требуемого натяга Исходя из условия несдвигаемости, минимально допустимое давление в контакте
Здесь
Подставляя в выражение для определения давления числовые значения входящих в него величин, получаем:
Условие нераскрытия соединения с натягом при одновременном приложении радиальной силы и изгибающего момента записывается следующим образом (4.2.22):
или
2.2. Соединения деталей вращения 99
где наибольшее значение давления, создаваемого радиальной силой; - наибольшее значение давления,создаваемого моментом изгиба; коэффициент запаса по нераскрытию, Кс = 1,8.
Минимально необходимое давление для отсутствия зазоров в стыке, найденное из условия нераскрытия, равно
Видно, что минимальное давление много меньше давления вательно, дальнейший расчет будем вести по давлению Теперь необходимо вычислить расчетный натяг задачи Ляме контакта двух толстостенных цилиндров (4.2.6), когда внутренний диаметр одного из цилиндров (в нашем случае — вала) равен нулю. Если обозначить вал как деталь 1, а колесо— как деталь 2, то решение задачи Ляме будет иметь вид:
где
стоянные величины, определяемые по формулам 2.8.20: 100 Глава 2. Соединения элементов машин Для того чтобы получить величину требуемого минимального натяга обходимо к значению расчетного натяга прибавить величину поправки и на шероховатость (4.2.7):
Определение максимально допустимого натяга Помимо минимально необходимого натяга для данного типа соединений большое значение имеет также величина максимально допустимого натяга. Под максимально допустимым понимается натяг, при котором эквивалентные напряжения в самых нагруженных точках соединения будут равняться пределу текучести материала детали. Таким образом, необходимо проверить соединение на отсутствие пластических деформаций. Наибольшие эквивалентные напряжения возникают в точках внутренних поверхностей вала и втулки (т. е. в данном случае червячного колеса). Максимально допустимое давление в контакте для вала (4.2.11):
Максимально допустимое давление в контакте для втулки:
Максимально допустимый натяг определяем как наименьшее из полученных давлений: Максимальный расчетный натяг:
Максимально допустимый натяг:
Для требуемых параметров, ка ный натяг
|

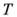 =960 Нм; радиальная сила
=960 Нм; радиальная сила 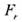 =2936 Н; осевая сила
=2936 Н; осевая сила 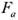 =1852 Н; опрокидывающий момент М = 222 Нм.
=1852 Н; опрокидывающий момент М = 222 Нм.
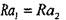 = 1,6 мкм, сборка осуществляется под прессом.
= 1,6 мкм, сборка осуществляется под прессом. = 355 МПа; модуль упругости
= 355 МПа; модуль упругости
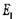 = 2,1 • 105 МПа; коэффициент Пуассона
= 2,1 • 105 МПа; коэффициент Пуассона 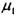 = 0,3), центр колеса отлит из чугуна
= 0,3), центр колеса отлит из чугуна рассчитывается по формуле 4.2.5:
рассчитывается по формуле 4.2.5: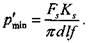
 = 0,1 — коэффициент трения в контакте сопрягаемых деталей;
= 0,1 — коэффициент трения в контакте сопрягаемых деталей; 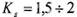 — коэффициент запаса сцепления (в данной задаче примем
— коэффициент запаса сцепления (в данной задаче примем  = 1,8);
= 1,8); 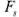 — наибольшее усилие сдвига, величина которого определяется как результат векторного сложения внешней осевой
— наибольшее усилие сдвига, величина которого определяется как результат векторного сложения внешней осевой 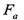 и окружной
и окружной 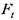 (от момента вращения) сил:
(от момента вращения) сил:
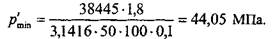
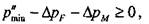
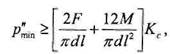
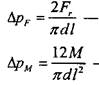
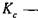
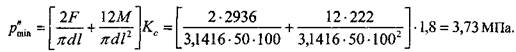
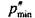 , найденное из условия нераскрытия,
, найденное из условия нераскрытия,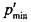 , рассчитанного по критерию несдвигаемости. Следо-
, рассчитанного по критерию несдвигаемости. Следо- = 44,05 МПа.
= 44,05 МПа.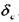 , который обеспечит наличие в соединении давления
, который обеспечит наличие в соединении давления  . Расчетный натяг можно найти, решая частный случай
. Расчетный натяг можно найти, решая частный случай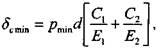
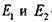 — модули упругости сопряженных деталей,
— модули упругости сопряженных деталей, 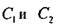 — некоторые по-
— некоторые по-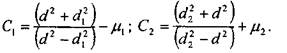
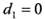 , то
, то


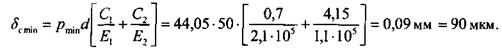
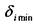 , не-
, не-
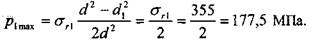

 =98 МПа.
=98 МПа.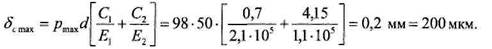
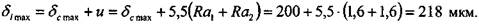
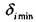 = 108 мкм и
= 108 мкм и 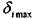 =218 мкм, подходит посад-
=218 мкм, подходит посад-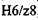 , которая обеспечивает минимальный натяг=
, которая обеспечивает минимальный натяг= 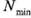 120 мкм и максималь-
120 мкм и максималь-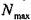 =175 мкм.
=175 мкм.


