ПРАКТИЧЕСКАЯ ЧАСТЬ. Пример 1. Написать рекурсивную функцию определения наибольшего общего делителя двух целых чисел.
Пример 1. Написать рекурсивную функцию определения наибольшего общего делителя двух целых чисел. Программный код решения примера
Решение примера выполнено на основе простой хвостовой рекурсии, поскольку значения вызовов функции самой себя gcd(b, a % b) возвращаются оператором return. Известно, что если даны два числа А и В, то максимальный остаток от деления числа А на число В будет на единицу меньше числа В. В определении рекурсивной функции gcd() условием останова является то, что остаток от деления двух данных чисел равен нулю. Рекурсивные вызовы функции gcd() связаны с изменением расположения первоначально заданных аргументов, когда аргумент, стоящий на втором месте (b), будет на первом месте, а на втором месте определяется операция остатка от деления, т. е. a%b. И это происходит до тех пор, пока остаток от деления не станет равным нулю, т. е. выполнится условие останова (базовое условие). Возможный результат выполнения программы приведен на рис. 18.1.
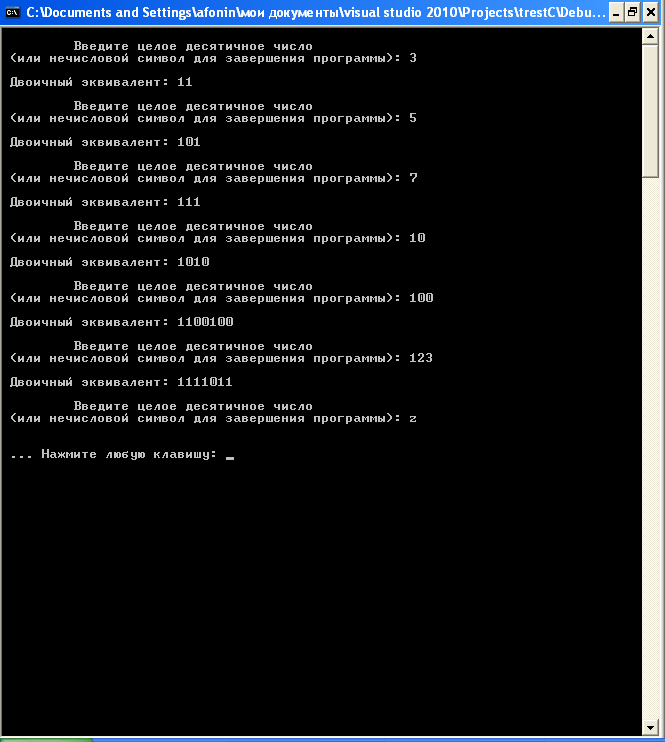
Задание 1 1. В программе оператор if используйте для рекурсивных вызовов, а оператор else – как условие останова. 2. B программу включите определение количества рекурсивных вызовов. 3. Видоизмените программу для случая ошибочного ввода чисел, предусмотрите повторное приглашение на ввод чисел. 4. Напишите функцию вычисления наибольшего общего делителя на основе итерации (с использованием операторов цикла). Пример 2. Написать рекурсивную функцию, которая выводит на консоль двоичный эквивалент целого десятичного числа, введенного пользователем с клавиатуры. Для решения примера отметим, что в двоичной системе счисления числа представлены в виде суммы степеней 2. Подобно тому, как в десятичной системе счисления число 234 означает 2×102 + 3×101 + 4×100, число 101 в двоичной системе означает 1×22 + 0×21 + 1×20 [7]. В двоичных числах используются только цифры 0 и 1. Очевидно, что за основу решения примера следует брать целочисленное деление. Если введено число n, то оно может быть либо четным, либо нечетным. Тогда остаток от деления на 2 будет равняться нулю для четных чисел и единице – для нечетных. Программный код решения примера
В программе шаги рекурсии осуществляются при условии, что аргумент рекурсивной функции больше или равен двум. Как только это условие нарушается, происходит распечатка результата и выход из функции. Например, при n = 10 остаток от целочисленного деления r = 10%2 = 0. В то же время аргумент функции dec2bin() будет равняться 5. Тогда остаток от целочисленного деления r = 5%2 = 1. Далее аргумент функции будет равняться 2 (5/2), так как аргумент функции определен через целое число. Остаток от целочисленного деления r = 2%2 = 0. Теперь аргумент рекурсивной функции будет равен 1, что прерывает рекурсивные вызовы функции (нарушается условие проверки оператором if). Остаток от деления r = 1%2 = 1. Вывод результата на консоль будет осуществляться из стека по дисциплине LIFO (Last Input First Output – последним вошел, первым вышел). Пример выполнения программы показан на рис. 18.2.
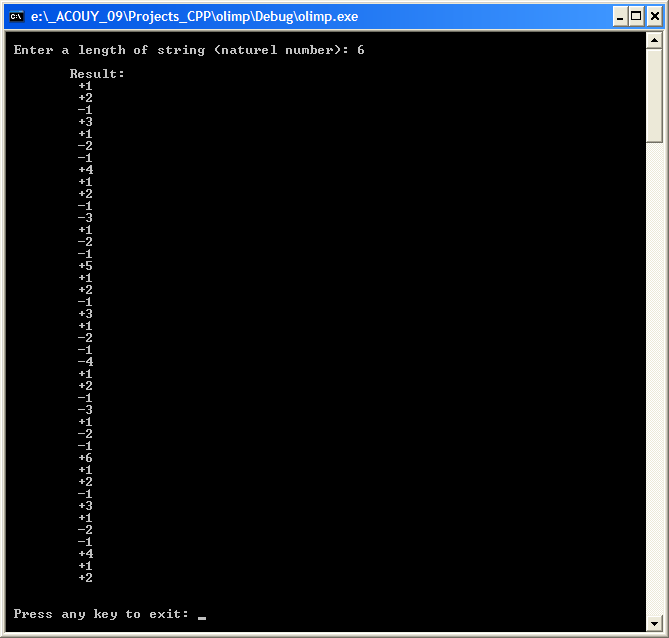
Задание 2 1. Определите, какой тип рекурсии используется в приведенной программе. 2. В программу включите защиту от ввода отрицательных целых чисел. 3. Вывод результатов преобразования десятичных чисел в двоичные эквиваленты осуществите в текстовый файл с именем compX.txt, где Х – номер компьютера, на котором выполняется лабораторная работа. В текстовый файл занести также и преобразуемое десятичное число. 4. В программе вместо функции printf() как функции вывода результата примените функцию putchar(). 5. В программу внесите изменения для подсчета количества рекурсивных вызовов. 6. Напишите программу преобразования десятичного числа в двоичный эквивалент не на основе рекурсивного подхода, а с помощью операций с разрядами. 7. Напишите программу с рекурсивной функцией вывода на консоль десятичного числа для введенного пользователем его двоичного эквивалента. Пример 3. С использованием косвенной рекурсии написать программу по решению следующей задачи. Строка состоит из клеток, пронумерованных от 1 до n. Состояние клетки можно изменить: если она пуста, поставить в нее шашку (занять ее), иначе убрать из нее шашку (освободить ее). Вначале строка пуста. Нужно занять все клетки, соблюдая правило: изменение клетки допустимо, если она имеет номер 1 или расположена непосредственно после занятой клетки, имеющей минимальный номер среди занятых клеток. Вход. Целое n, 1 £ n £ 15. Выход. Последовательность элементов вида + i или – i, обозначающих соответственно занять клетку i и освободить клетку i [9]. Например, при n = 3 выход имеет вид +1+2–1+3+1. Программный код решения примера [см. 9]
В программе вывод результата на консоль выполнен в виде столбца. Для этого используется эскейп-последовательность \t в функциях printf(). Форматный вывод значений в функциях printf() выполнен с помощью спецификации %+3d, что позволяет автоматически устанавливать знаки чисел, под которые отводятся 3 позиции. Как видно из приведенного программного кода, в каждой из функций имеется вызов самой функции и других функций. Это указывает на косвенное обращение к функциям. Результат выполнения программы представлен на рис. 18.3.
Задание 3 1. В программе укажите рекурсивные функции. Объясните их работу. 2. Проверьте работу программы при смене порядка объявлений функций. 3. Проверьте работу программы без использования прототипов функций. 4. Для случая, когда n £ 5, предусмотрите вывод результата в строку, а не в столбец. 5. В программу добавьте программный код для подсчета рекурсивных вызовов каждой из рекурсивных функций. 6. Постройте зависимость количества рекурсивных вызовов одной из функций от введенного числа n. 7. Постройте зависимость числа комбинаций заполнения и освобождения клеток от введенного числа n.
Пример 4. Написать программу по решению задачи «Ханойская башня». Имеется пирамида из n колец, лежащих на основании А (на стержне, на столбе) одно на другом в порядке убывания размеров. Кольца должны быть перемещены на основание В в том же порядке, в котором они были на основании А, при использовании промежуточного основания С. Единственными разрешенными перемещениями являются такие, при которых кольцо, взятое с вершины одной из пирамид, помещается на большее кольцо, либо на пустое основание. Осуществить выдачу на печать (на консоль, в текстовый файл) последовательности перемещений колец. Алгоритм решения этой задачи достаточно подробно описан в работе [10]. Решение задачи «Ханойская башня» Для рекурсивного решения задачи следует пройти три этапа. 1-й этап – параметризация. Естественным параметром является n – число колец. В число параметров можно включить также три основания: А (исходное), В (конечное), С (промежуточное). 2-й этап – поиск тривиальных случаев. Здесь тривиальным случаем будет такой, при котором n = 0; тогда просто нечего делать. 3-й этап – редукция общего случая к более простому. Здесь надо отметить, что n колец могут быть перемещены с А на В следующим путем: · переноса (рекурсивно) n – 1 колец с вершины А (исходное основание) на С (промежуточное основание) с учетом правил: основание В (конечная цель) используется как промежуточное; · перемещения на В кольца наибольшего диаметра, оставшегося на А; · переноса (рекурсивно) n – 1 других колец с С на В при соблюдении правил с А в качестве промежуточного основания. Алгоритм решения задачи запишем в следующем виде: hanoi(n–1, A, C, B); переместить (A, B); hanoi(n–1, C, B, A); где hanoi() – имя рекурсивной функции [10]. Пример промежуточного положения Ханойской башни при n = 4 показан на рис. 18.4.
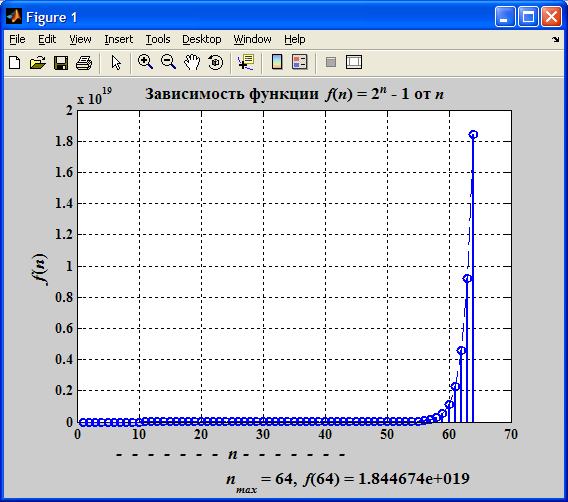
Рис. 18.4. Промежуточное положение Ханойской башни при n = 4 Число элементарных перемещений равно
На рис. 18.5 приведена зависимость элементарных перемещений от числа дисков.
С учетом того что перемещение диска есть рекурсивный вызов функции, то на каждый вызов требуется определенное время. Практически с любым конечным малым временем обработки рекурсивного вызова общее время работы рекурсивной функции для большого количества дисков n становится невыполнимым на существующих компьютерах. В соответствии с легендой конец света наступит при перемещении 64 дисков [10]. В связи со степенным ростом числа рекурсивных вызовов в программе ограничимся величиной n = 15. Программный код решения примера
Результат выполнения программы при n = 5 показан на рис. 18.6.
Задание 4 1. Определите тип рекурсии, используемой в программе. 2. Для случая, когда не все элементарные перемещения выводятся на экран дисплея, предусмотрите вывод результата программы в текстовый файл с именем compX.txt, где X – номер компьютера, на котором выполняется лабораторная работа. 3. Программным путем выполните подсчет общего количества обращений к рекурсивной функции. Сделайте также вывод порядкового номера перемещения на экран дисплея. Порядковый номер расположите слева от элементарного перемещения. Постройте (в MS Excel или в MATLAB) зависимость количества обращений к рекурсивной функции от заданного числа дисков. 4. Измените аргументы рекурсивной функции: включите переменные типа int для определения имени (нумерации) основания. 5. Измените условие задачи «Ханойская башня». Сначала исходным основанием считайте В, конечным – С, промежуточным – А. Затем примите за исходное основание С, промежуточное – В, конечное – А.
Пример 5. «Задача о рюкзаке». Есть 10 предметов, о которых известны их массса и стоимость. Требуется поместить в рюкзак предметы таким образом, чтобы они не превысили допустимую массу для рюкзака при максимальной стоимости выбранных предметов. Исходные параметры модели – характеристики предметов приведены в табл.18.1 [11].
Данная задача широко известна [9–11], она еще называется задачей о ранце, или в английском произношении – «knapsack problem». Предполагается, что один и тот же предмет не может быть взят несколько раз. Для решения поставленной задачи используем рекурсивный алгоритм, описанный в работе [11], где также приводится фрагмент программы на языке программирования MODULA – 2. Программный код решения примера
Пример выполнения программы представлен на рис. 18.7.
Представленная программа основана на следующем алгоритме [11]. В рекурсивной функции TRY() определены две ситуации для выбора предмета в рюкзак. Если речь идет о включении, то объект (предмет со своей массой и стоимостью) можно включить в выборку для укладки в рюкзак, если он подходит по массовым ограничениям. Если он не подходит, то попытки добавить еще один объект в текущую выборку можно прекратить. Когда же речь идет об исключении, то критерием приемлемости, т. е. возможности продолжения построения текущей выборки, будет то, что после данного исключения общая ценность (стоимость) будет не меньше полученного до этого момента оптимума. В данной программе реализована схема с возвратами, использующая некоторые ограничения для уменьшения роста потенциального дерева поиска, называется она алгоритмом ветвей и границ [11]. Задание 5 1. Подсчитайте количество рекурсивных вызовов функции TRY() в зависимости от величины допустимой массы рюкзака, начиная от 10 и до 120 с шагом в 10 условных единиц. Постройте график полученной зависимости (в MS EXCEL или в MATLAB). 2. Рекурсивную функцию TRY() расположите в отдельном файле с именем compX.c, где Х – номер компьютера, на котором выполняется лабораторная работа. 3. Сформирйте массив данных о предметах по случайному равномерному закону из интервала [10; 20Х], где Х – номер компьютера, на котором выполняется лабораторная работа. Размер массива выберите случайно из интервала натуральных чисел [10; 18]. 4. В программу внесите изменения, которые позволили бы определить номера предметов, отобранных в рюкзак. Соответственно укажите массу и стоимость каждого предмета. Пример 6. Написать программу сортировки одномерного массива целых чисел на основе рекурсивного алгоритма быстрой сортировки Хоара. Суть алгоритма быстрой сортировки заключается в следующем. Выбираем наугад какой-либо элемент х исходного массива. Будем просматривать слева наш массив до тех пор, пока не встретим элемент ai > x, затем будем просматривать массив справа, пока не встретим ai £ х. Поменяем местами эти два элемента и продолжим процесс просмотра и обмена до тех пор, пока оба просмотра не встретятся. В результате исходный массив окажется разбитым на две части, левая будет содержать элементы меньше или равные х, а правая – элементы больше х. Применив процедуру разделения к левой и правой частям массива от точки встречи, получим четыре части и т. д., пока в каждой из них не окажется только один элемент [12]. В качестве граничного элемента х для разделения обычно выбирают средний элемент массива. Программный код решения примера
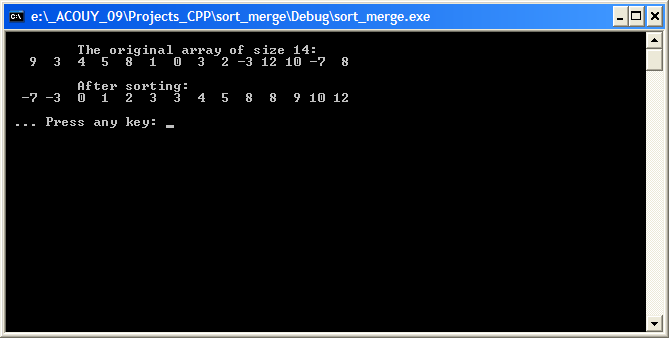
Рис. 18.8. Пример быстрой сортировки одномерного массива Задание 6 1. В программу внесите изменения для сортировки вещественных данных. 2. В программу внесите изменения для сортировки массива по убыванию. 3. Рекурсивную функцию программы разместите во внешнем файле с именем compX.c, где Х – номер компьютера, на котором выполняется лабораторная работа. 4. Размерность массива, подлежащего сортировке, и данные массива задайте случайно из интервалов [10; 100] и [10Х; 50Х], где Х – номер компьютера, на котором выполняется лабораторная работа. 5. Подсчитайте количество рекурсивных вызовов при сортировке массивов, задаваемых случайным образом. Пример 7. Написать программу сортировки одномерного массива целых чисел на основе рекурсивного алгоритма слиянием. При алгоритме слиянием сортировку производят по частям, а затем отдельные части соединяют в единое целое [5]. Выберем следующую схему разбиения данных. Будем разрезать массив данных на две равные части, образуя два подмассива. Затем сортировка слиянием рекурсивно вызывает себя для каждого из двух подмассивов. Конечным шагом является слияние двух сортированных подмассивов в один сортированный массив [13]. Особенностью алгоритма слиянием является то, что при сортировке требуется временный массив для результата. Данный алгоритм может быть использован при сортировке внешних данных, например, записанных в отдельные файлы [5]. Программный код решения примера
Рис. 18.9. Пример сортировки слиянием одномерного массива В алгоритме сортировки слиянием можно выделить три этапа. 1. Сортируемый массив разбивается на две половины примерно одинакового размера. 2. Каждая из получившихся половин сортируется отдельно (каким-либо известным алгоритмом, в том числе с помощью алгоритма слиянием). 3. Два упорядоченных массива половинного размера соединяются в один. Рекурсивное разбиение заданного массива происходит до тех пор, пока размер массива не достигнет единицы. Далее решается нетривиальная задача соединения двух упорядоченных массивов в один. Алгоритм сортировки слиянием был предложен Джоном фон Нейманом в 1945 г. Такая сортировка считается предпочтительной в случае, когда требуется застраховаться от наихудшего случая, возможного при использовании быстрой сортировки [12]. Задание 7 1. Все вспомогательные функции программы разместите во внешние файлы с именами compX_1.c, compX_2.c и т. д., где Х – номер компьютера, на котором выполняется лабораторная работа. Протестируйте программу на примере и подсчитайте количество рекурсивных вызовов. 2. Подготовьте два неотсортированных массива и произведите их слияние в один отсортированный массив. Данные массивов задаются случайно по равномерному закону из интервалов [–5Х; 5Х] и [0; 10Х], где Х – номер компьютера, на котором выполняется лабораторная работа. Размерности массивов должны задаваться с клавиатуры. 3. Напишите программу по сортировке слиянием двух массивов, расположенных в текстовых файлах (внешняя сортировка слиянием). Результат сортировки разместите также в текстовый файл с именем compX.txt, где Х – номер компьютера, на котором выполняется лабораторная работа.
Контрольные вопросы 1. Когда следует применять рекурсивные алгоритмы? 2. Какие методы и приемы устранения «хвостовой» рекурсии Вам известны? 3. Какие проблемы могут возникать при реализации рекурсивных алгоритмов на электронных вычислительных машинах? 4. В чем отличие глубины рекурсии от рекурсивного вызова? 5. В каких задачах в программировании применение рекурсии оправдано?
|


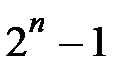 , где n – количество исходных дисков [10]. С увеличением n число перемещений быстро нарастает.
, где n – количество исходных дисков [10]. С увеличением n число перемещений быстро нарастает.