Решение системы линейных уравнений методом обратной матрицы
Дана система уравнений (9). Решение: Пусть A= (10) – основная матрица системы, Х – матрица-столбец неизвестных системы (9), В – матрица-столбец свободных членов системы (9)
значит
Найдем определитель матрицы А
Для нахождения матрицы вычислим алгебраические дополнения для элементов матрицы А
Построим матрицу
Найдем транспонированную матрицу
Найдем обратную матрицу
Произведем проверку обратной матрицы, с помощью произведения матрицы на обратную матрицу и наоборот, если результат в обои случаях будет равен единичной матрице, значит обратная матрица найдена верно
С=
С=
Верно, обратная матрица найдена, вычислена правильно.
Находим решение матрицы
Проверка: решенная система ранее была решена методом Крамера с проверкой, решение (текущей) системы методом обратной матрицы совпадает с решением методом Крамера. Вывод системы решены верно, ответ:
|

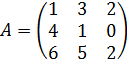 , (12)
, (12)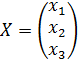 , (13)
, (13) , (14)
, (14)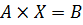 (15)
(15)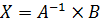 (16)
(16)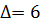

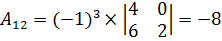
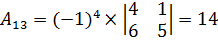



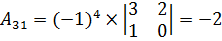


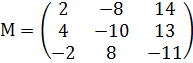
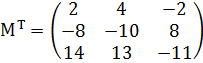




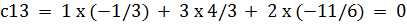
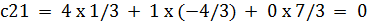

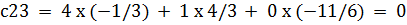

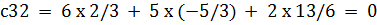 c33 = 6 x (-1/3) + 5 x 4/3 + 2 x (-11/6) = 1
c33 = 6 x (-1/3) + 5 x 4/3 + 2 x (-11/6) = 1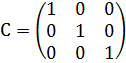 = Е
= Е



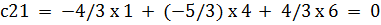

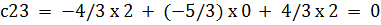

 c33 = 7/3 x 2 + 13/6 x 0 + (-11/6) x 2 = 1
c33 = 7/3 x 2 + 13/6 x 0 + (-11/6) x 2 = 1 =
=  ;
;



