Решение систем линейных уравнений методом Гаусса
Метод Гаусса — классический метод решения системы линейных алгебраических уравнений (СЛАУ). Состоит в постепенном понижении порядка системы и исключении неизвестных. Хотя в настоящее время данный метод повсеместно называется методом Гаусса, он был известен и до К. Ф. Гаусса. Первое известное описание данного метода — в китайском трактате «Математика в девяти книгах», составленном между I в. до н.э. и II в. н. э. Описание метода: Пусть исходная система будет представлена в следующем виде:
Тогда согласно свойству элементарных преобразований над строками эту систему можно привести к виду трапеции:
Переменные Если Предположим, что Перенесем свободные переменные за знаки равенств и поделим каждое из уравнений системы на свой коэффициент при самом левом
где Если свободным переменным системы придавать все возможные значения и вычислить через них главные переменные, то мы получим все решения этой СЛАУ. Так как эта система получена путем элементарных преобразований над исходной системой, то по теореме об эквивалентности при элементарных преобразованиях полученное нами решение является решением системы.
· Если в совместной системе все переменные главные, то такая система является определенной. · Если количество переменных в системе превосходит число уравнений, то такая система является либо неопределенной, либо несовместной. Условие совместности: Упомянутое выше условие
|


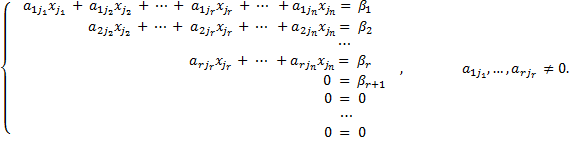
 называются главными переменными. Все остальные называются свободными.
называются главными переменными. Все остальные называются свободными.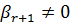 , то рассматриваемая система несовместна.
, то рассматриваемая система несовместна. .
. :
:
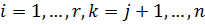 .
.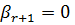 может быть сформулировано в качестве необходимого и достаточного условия совместности (рангом совместной системы называется ранг ее основной матрицы (либо расширенной, так как они равны)).
может быть сформулировано в качестве необходимого и достаточного условия совместности (рангом совместной системы называется ранг ее основной матрицы (либо расширенной, так как они равны)).


