Метод Крамера. Для решения квадратных систем линейных уравнений вида:
Для решения квадратных систем линейных уравнений вида:
с невырожденной основной матрицей используется теорема Крамера: Если основная матрица квадратной системы линейных уравнений невырожденная, то такая система имеет единственное решение Доказательство. Пусть A - основная матрица системы (1), Δ - ее определитель (главный определитель системы), X - столбец из ее неизвестных и B — столбец свободных членов системы. Тогда уравнение
представляет собой матричную запись системы (4.4). Так как по условию теоремы A — невырожденная матрица, то она имеет обратную A-1. Умножим обе части равенства (2) слева на A -1 (AX) = A -1 B (3) Используя ассоциативность умножения матриц, получаем (A -1 A)X = EX = X = A -1 B (4) Таким образом, X = A -1 B (5) Произведение, стоящее справа, будет матрицей из одного столбца. Ее j - й элемент равен сумме произведений j - й строки матрицы A -1 на соответствующие элементы матрицы B, т. е. равен числу
Сумма, стоящая в числителе справа, является, однако, разложением по j - му столбцу определителя Δ, получающегося заменой j - гo столбца определителя Δ столбцом B. Покажем, что полученные значения неизвестных действительно составляют решение системы (4). Для этого подставим вместо X в матричное уравнение (2) правую часть уравнения (5),
что приводит к тождеству B = B. Единственность решения системы (1) следует из единственности обратной матрицы A -1 и однозначности произведения матриц A -1B. Учитывая (6), запишем равенства соответствующих элементов матриц — столбцов, расположенных в левой и правой частях матричного равенства (2)
где Δ j - определители, получающиеся из Δ заменой j - го столбца определителя Δ столбцом B. Равенства (8) называются формулами Крамера решения квадратных систем линейных уравнений, основная матрица которых невырожденная. Если определитель основной матрицы квадратной системы линейных уравнений равен нулю, то теорему Крамера для нахождения решений системы применять нельзя.
|

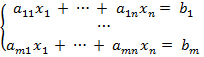 (1)
(1) (2)
(2)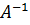 :
:


