Решение систем линейных уравнений методом обратной матрицы
Определение:если существуют квадратные матрицы B и А одного порядка, удовлетворяющие условию: BA = AB = E, где Е — единичная матрица того же самого порядка, что и матрица А, то матрица B называется обратной к матрице А и обозначается А-1. Каждая квадратная матрица с определителем, не равным нулю имеет обратную матрицу и притом только одну. Вычисление обратной матрицы Рассмотрим квадратную матрицу
Обозначим Квадратная матрица А называется невырожденной, или неособенной, если ее определитель отличен от нуля, и вырожденной, или особенной, если Теорема. Для того чтобы матрица А имела обратную, необходимо и достаточно, чтобы ее определитель был отличен от нуля. Матрица, обратная матрице А, обозначается через
где Для нахождения обратных матриц больших порядков, обычно применяют следующую формулу
|
.
.
.
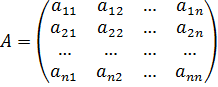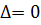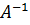, так что 
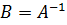. Обратная матрица вычисляется по формуле
,
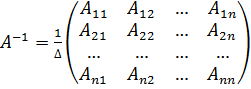— алгебраические дополнения элементов 
.
, где 
— дополнительный минор элемента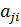 
матрицы А.
