Что называется системой линейных уравнений
СОДЕРЖАНИЕ СОДЕРЖАНИЕ.. 2 ВВЕДЕНИЕ.. 3 1 ТЕОРИТИЧЕСКАЯ ЧАСТЬ.. 4 1.1 Что называется системой линейных уравнений. 4 1.2 Методы решения систем линейных уравнений. 5 1.2.1 Метод Крамера. 5 1.2.2 Решение систем линейных уравнений методом обратной матрицы.. 7 1.2.3 Решение систем линейных уравнений методом Гаусса. 8 2 ПРАКТИЧЕСКАЯ ЧАСТЬ.. 10 2.1 Решение системы линейных уравнений методом Крамера. 10 2.2 Решение системы линейных уравнений методом обратной матрицы.. 11 2.3 Решение системы линейных уравнение методом Гаусса. 14 ЗАКЛЮЧЕНИЕ.. 17 СПИСОК ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВ.. 19
ВВЕДЕНИЕ Целью курсовой работы является закрепление и углубление студентом полученных и теоретических знаний и практических навыков по решению систем линейных уравнений, следующими методами: методом Гаусса, методом Крамера и с помощью обратной матрицы.
ТЕОРИТИЧЕСКАЯ ЧАСТЬ Что называется системой линейных уравнений Системой m линейных уравнений с n неизвестными называется система вида:
где Коэффициенты при неизвестных будем записывать в виде матрицы
которую назовем матрицей системы. Числа, стоящие в правых частях уравнений, Наша задача будет заключаться в нахождении решений системы. При этом могут возникнуть три ситуации: 1. Система может иметь единственное решение. 2. Система может иметь бесконечное множество решений. Например,
решением которой является любая пара чисел, отличающихся знаком. 3. И третий случай, когда система вообще не имеет решения. Например,
если бы решение существовало, то Система линейных уравнений, имеющая хотя бы одно решение, называется совместной. В противном случае, т.е. если система не имеет решений, то она называется несовместной.
|


 и
и  (i =1,…, m; b =1,…, n) — некоторые известные числа, а
(i =1,…, m; b =1,…, n) — некоторые известные числа, а  — неизвестные. В обозначении коэффициентов
— неизвестные. В обозначении коэффициентов  ,
,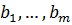 называются свободными членами. Совокупность n чисел
называются свободными членами. Совокупность n чисел  называется решением данной системы, если каждое уравнение системы обращается в равенство после подстановки в него чисел
называется решением данной системы, если каждое уравнение системы обращается в равенство после подстановки в него чисел 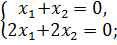
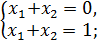
 равнялось бы одновременно нулю и единице.
равнялось бы одновременно нулю и единице.


