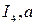Эквивалентного генератора
Метод эквивалентного генератора является частным случаем метода преобразования (метода эквивалентных цепей) и базируется на теореме об эквивалентном генераторе. Эта теорема гласит: по отношению к одной выделенной ветви Сопротивление r э равно сопротивлению преобразуемой части сложной цепи относительно полюсов Применение метода для расчета цепей рассмотрим на следующем примере. Дана схема цепи (рисунок 2.1) с известными источниками ЭДС и сопротивлениями ветвей. Требуется найти ток I ab, протекающий через сопротивление r. Для определения тока в ветви методом эквивалентного генератора: · заменим часть сложной цепи (обведенную пунктиром) эквивалентным источником ЭДС., с ЭДС E э12 и внутренним сопротивлением r э (рисунок 2.2); на этом рисунке эквивалентный генератор отмечен пунктиром; · отключив ветвь · отключив ветвь · по закону Ома найдем ток в ветви I ab= Если ветвь I ab= Расчет
Рисунок 2.3 – Схема эквивалентного источника
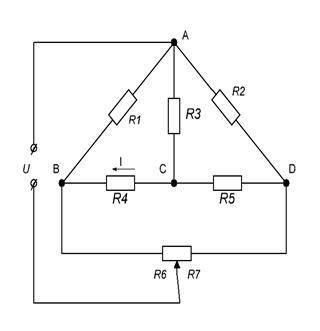
Рисунок 2.4 - Электрическая схема ЭДМУ Иногда целесообразно при расчетах (в особенности в схемах с электронными и полупроводниковыми элементами) заменить активный двухполюсник не эквивалентным генератором э. д. с, а эквивалентным генератором тока. В этом случае неизменная сила тока генератора будет I э= а сопротивление Пример. Определить ток Ток I в рамке логометра I = Определим
Рис 2.5 схема для определения UВСХХ на рамке логометра R4
Рисунок 2.6 – Схема для определения U вскз Рисунок 2.7 – Эквивалентная схема
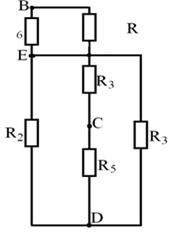
Определим потенциалы точек В и С
где
или
Аналогично определяется
где
и
Тогда
Определяем
Определим
Определяем ток
Аналогично приведенному определяется ток в сопротивлении При расчете логометра указателя необходимо знать соотношение токов в рамках
Обычно Задаваясь различными значениями сопротивления
Полученные результаты записываем в табл. 2.1. Таблица 2.1.
|

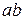 с сопротивлением r вся остальная часть сколь угодно сложной цепи (рисунок 2.1), содержащая сопротивления и источники ЭДС может быть заменена одним эквивалентным генератором (рисунок 2.2) с ЭДС E э12 и внутренним сопротивлением r э. ЭДС E э12, равная напряжению U ab.хх холостого хода между полюсами
с сопротивлением r вся остальная часть сколь угодно сложной цепи (рисунок 2.1), содержащая сопротивления и источники ЭДС может быть заменена одним эквивалентным генератором (рисунок 2.2) с ЭДС E э12 и внутренним сопротивлением r э. ЭДС E э12, равная напряжению U ab.хх холостого хода между полюсами  и
и 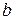 ;
;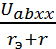
 , содержит источник с ЭДС.
, содержит источник с ЭДС. 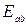 и внутренним сопротивлением
и внутренним сопротивлением 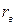 (рисунок 2.3), то ток в ветви
(рисунок 2.3), то ток в ветви 
 и r часто относительно сложен. Тем не менее применение данного метода существенно упрощает вычисления, особенно в тех случаях, когда нужно определить силу тока I ab при нескольких значениях сопротивления r m
и r часто относительно сложен. Тем не менее применение данного метода существенно упрощает вычисления, особенно в тех случаях, когда нужно определить силу тока I ab при нескольких значениях сопротивления r m
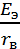 ,
, соединяется параллельно этому источнику тока.
соединяется параллельно этому источнику тока. в схеме ЭДМУ (рисунок 2.4).
в схеме ЭДМУ (рисунок 2.4). по методу эквивалентного генератора определяется
по методу эквивалентного генератора определяется ,
, . Для этого удобно схему ЭДМУ (рисунок 2.4) представить в виде рисунок2.5 U всхх= U в
. Для этого удобно схему ЭДМУ (рисунок 2.4) представить в виде рисунок2.5 U всхх= U в 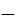 U c
U c


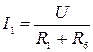
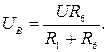


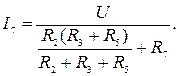
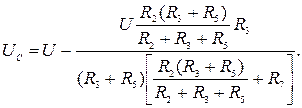

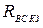 . Для этого преобразуем схему, как показано на рис. 2.6 и 2.7, где
. Для этого преобразуем схему, как показано на рис. 2.6 и 2.7, где


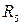 ,которое, как и
,которое, как и  и
и  . Эти сопротивления являются плечами потенциометра датчика. Поэтому
. Эти сопротивления являются плечами потенциометра датчика. Поэтому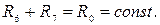
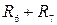 выбирают равным 250 – 260 Ом.
выбирают равным 250 – 260 Ом.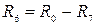 (шесть-восемь точек), можно получить искомые токи в сопротивлениях
(шесть-восемь точек), можно получить искомые токи в сопротивлениях