Указателя манометра типа ЭДМУ
Логометр манометра типа. ЭДМУ представляет собой совокупность двух неподвижных катушек с током расположенных под углом 120°, и подвижного магнита, вращающегося внутри катушек (рис. 2.8) [25]. Для осуществления электромагнитного демпфирования подвижный магнит расположен в медном стакане. Для защиты от внешних магнитных полей катушки с магнитом расположены внутри экрана, изготовленного из пермаллоя. При расчете логометра предполагается, что все основные геометрические размеры известны. Необходимо определить моменты, действующие в логометре, и основные критерии качества логометра: добротность прибора, характеристику шкалы, а также определить некоторые электрические параметры логометра и влияние дополнительного магнита на показания логометра.
Определение некоторых электрических параметров логометра [10] При расчете задаются геометрические размеры катушек, исходя из конструктивных размеров магнита и указателя. Полное сопротивление катушки
Рис. 2.8. Магнитоэлектрический логометр с подвижным магнитом: 1 – медный корпус магнитного успокоителя; 2 – подвижный магнит; 3 – внутренняя катушка; 4 – неподвижный постоянный магнит; 5 – стрелка; 6 – корундовые подпятники; 7 – мостик; 8 – экран из пермаллоя; 9 – ось подвижной системы; 10 – внешняя катушка; 11 – керн оси подвижной системы.
Поскольку конструктивно две секции одной катушки находятся внутри другой, то высота а их будет различна и, следовательно, электрические параметры также будут разные. Средняя длина витка большей (первой) катушки
Сопротивление витка
где
Количество витков в секции катушки
Здесь
Площадь сечения намотки секции катушки
где
Аналогично проводится расчет меньшей (второй) катушки. Средняя длина витка второй катушки
Сопротивление катушки
Конструктивно для симметрии логометра берется равное количество витков в обеих рамках, т. е.
Моменты, действующие в логометре Взаимодействие постоянного магнита с магнитными полями двух катушек создает два вращающих момента, направленных в противоположные стороны- В положении равновесия моменты равны друг другу и, следовательно, устанавливающий момент, равный их разности, будет равен
Каждый из этих моментов
или где Выражение (2.6) обеспечивает достаточную точность расчета только в том случае, когда магнит вращается в однородном магнитном поле, т. е. когда геометрические размеры катушек намного больше размеров постоянного магнита. Поскольку в логометре имеются две катушки, создающие в сумме явно неравномерное поле, то при дальнейших расчетах будем пользоваться усредненным по всему внутреннему объему катушек значением результирующего магнитного поля. Для определения магнитного момента подвижного магнита необходимо найти его коэффициент размагничивания. Реальный магнит, представленный на рис. 2.9, с достаточной степенью точности может быть рассчитан по формулам для эллипсоида. Для вычисления коэффициентов размагничивания та эллипсоида с тремя различными осями воспользуемся формулой, выведенной на основании теоремы Пуассона для однородного намагниченного эллипсоида по продольной оси
где
Значения эллиптических интегралов определяются по математическим таблицам [11].
Зная коэффициент размагничивания подвижного магнита,, можно легко определить намагниченность магнита, а следовательно, и его магнитный момент:
где
Намагниченность магнита определяется графически по кривой размагничивания петли гистерезиса материала магнита (рис. 2.10) как точка пересечения кривой размагничивания и прямой, проведенной из начала координат под углом
где Кривую размагничивания по намагниченности
Кривая Расчет напряженности магнитного поля прямоугольной катушки конечной длины представляет определенную трудность. Поэтому целесообразно провести расчет прямоугольной катушки по эквивалентной ей круглой катушке, При этом должно соблюдаться равенство средних площадей катушек, длин и числа витков катушек. При определении размеров эквивалентной катушки принимаем, что длина и толщина круглой катушки соответствуют прямоугольной катушке.
Рис 2.11 подвижный магнит
Средний радиус круглой катушки определяется из условия равенства средних площадей (рис. 2.11).
или
где
Определение напряженности производится по формуле для многослойной катушки [7]:
где
Ввиду того, что каждая катушка в логометре состоит из двух секций, расположенных на расстоянии 1,5—2,5 мм друг от друга, для установки оси подвижной системы расчет проводится для двух секций. Средняя напряженность поля внутри объема, занимаемого магнитом, определяется как средняя арифметическая напряженность, вычисленная для двух секций в трех точках. В центре по оси подвижного магнита она равна сумме одинаковых напряженностей от двух секций.
В центрах обеих секций
Средняя напряженность поля на оси катушки в пределах от
Обозначив в формулах (2.10, 2.11) все постоянные величины, определяемые конструктивными размерами катушки, через постоянный коэффициент k можно записать
В логометре имеются две катушки, расположенные под углом 120° и вставленные друг в друга. Они, как отмечалось выше, создают два момента — вращающий и противодействующий, направленные навстречу друг другу:
где
Момент устанавливающий равен разности указанных моментов, т. е.
или
Измерительные механизмы характеризуются удельным устанавливающим моментом, который определяется как производная от устанавливающего момента по углу отклонения: подвижной части от положения равновесия
Коэффициент добротности прибора определяется для устанавливающего момента, соответствующего углу отклонения 90°.
где
При равновесии устанавливающий момент равен нулю, тогда
или, учитывая (2.12):
Откуда
Это выражение определяет зависимость угла поворота стрелки
|

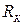 берется из расчета электрической схемы всего прибора, исходя из условия наибольшей чувствительности, т. е. сопротивление измерительного прибора должно быть равно выходному сопротивлению мостовой схемы. Диаметр провода катушки определяется из условия допустимой плотности тока 4 – 6 а/мм2.
берется из расчета электрической схемы всего прибора, исходя из условия наибольшей чувствительности, т. е. сопротивление измерительного прибора должно быть равно выходному сопротивлению мостовой схемы. Диаметр провода катушки определяется из условия допустимой плотности тока 4 – 6 а/мм2.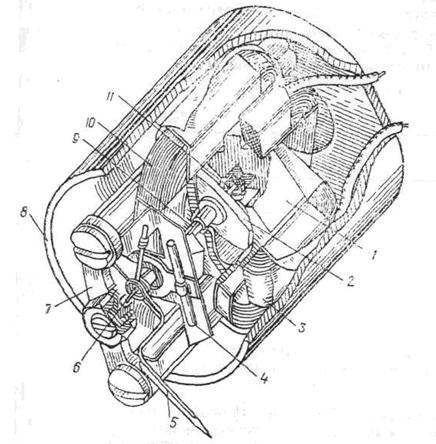
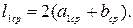
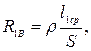 (2.1)
(2.1)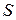 – площадь сечения провода;
– площадь сечения провода;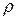 – удельное сопротивление.
– удельное сопротивление. (2.2)
(2.2)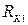 – сопротивление катушки, полученное из условия наибольшей чувствительности.
– сопротивление катушки, полученное из условия наибольшей чувствительности.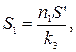 (2.3)
(2.3) – коэффициент заполнения, равный 0,7÷0,8;
– коэффициент заполнения, равный 0,7÷0,8;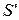 – площадь сечения провода с изоляцией.
– площадь сечения провода с изоляцией.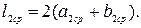
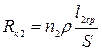 (2.4)
(2.4)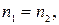 и одного и того же сечения провода
и одного и того же сечения провода 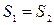 . Из этого же условия требуется выполнение равенства сопротивлений в плечах рамок, что достигается включением дополнительного сопротивления
. Из этого же условия требуется выполнение равенства сопротивлений в плечах рамок, что достигается включением дополнительного сопротивления 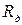 в цепь второй рамки, величина которого может быть определена:
в цепь второй рамки, величина которого может быть определена: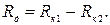
 (2.5)
(2.5)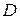 и
и  можно рассматривать, как момент, вызванный взаимодействием вектора магнитного момента постоянного магнита
можно рассматривать, как момент, вызванный взаимодействием вектора магнитного момента постоянного магнита 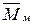 и вектора напряженности магнитного поля катушки
и вектора напряженности магнитного поля катушки 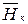 .
.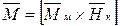
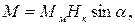 (2.6)
(2.6)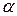 – угол между направлением векторов в плоскости, перпендикулярной к оси вращения магнита.
– угол между направлением векторов в плоскости, перпендикулярной к оси вращения магнита. [24]:
[24]: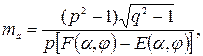 (2.7)
(2.7)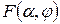 – эллиптический интеграл первого рода;
– эллиптический интеграл первого рода; – эллиптический интеграл второго рода.
– эллиптический интеграл второго рода.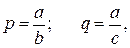
 – толщина магнита;
– толщина магнита;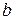 – ширина магнита;
– ширина магнита;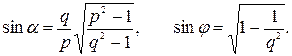
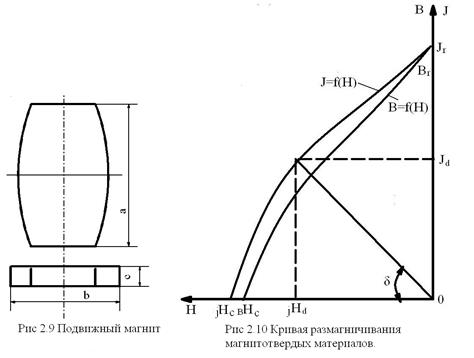
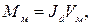 (2.8)
(2.8)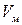 – объем магнита;
– объем магнита;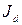 – намагниченность магнита.
– намагниченность магнита.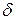 к оси абсцисс, причем тангенс этого угла равен
к оси абсцисс, причем тангенс этого угла равен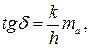
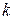 и
и 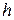 – масштабные коэффициенты соответственно по осям ординат и абсцисс.
– масштабные коэффициенты соответственно по осям ординат и абсцисс.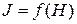 необходимо построить с помощью кривой размагничивания по индукции
необходимо построить с помощью кривой размагничивания по индукции 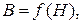 используя выражение
используя выражение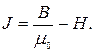 (2.9)
(2.9)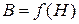 дается в справочных таблицах по магнитотвердым материалам [12].
дается в справочных таблицах по магнитотвердым материалам [12].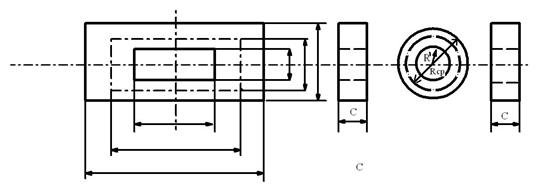
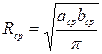
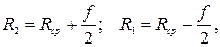
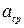 и
и 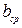 – средние размеры сторон прямоугольной катушки;
– средние размеры сторон прямоугольной катушки;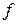 – толщина намотки катушки;
– толщина намотки катушки;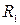 – внутренний радиус катушки;
– внутренний радиус катушки;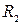 – внешний радиус катушки.
– внешний радиус катушки. (2.10)
(2.10)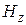 – напряженность поля в точках, лежащих на продольной оси катушки;
– напряженность поля в точках, лежащих на продольной оси катушки;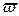 – плотность намотки катушки,
– плотность намотки катушки, 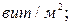
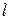 – длина катушки;
– длина катушки; – расстояние от центра катушки до точки на продольной ее оси, в которой вычисляется напряженность поля.
– расстояние от центра катушки до точки на продольной ее оси, в которой вычисляется напряженность поля.
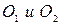

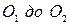 равна
равна (2.11)
(2.11)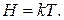 (2.12)
(2.12)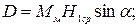
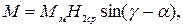 (2.13)
(2.13)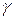 – уголмежду площадями катушек (120°);
– уголмежду площадями катушек (120°);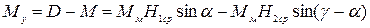
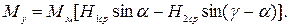 (2.13a)
(2.13a)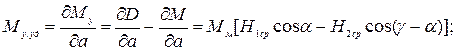 (2.14)
(2.14)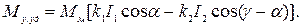
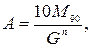 (2.15)
(2.15)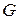 – вес подвижной части;
– вес подвижной части;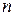 – показатель степени, равный 1,33—1,5. Для подвижной части, вес которой менее
– показатель степени, равный 1,33—1,5. Для подвижной части, вес которой менее 
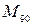 – устанавливающий момент для угла отклонения
– устанавливающий момент для угла отклонения 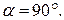 Из практического опыта известно, что наибольший коэффициент добротности при прочих равных условиях будет в. том случае, когда вес магнита в два раза больше веса подвижной системы (оси, стрелки, противовесы и т. д.).
Из практического опыта известно, что наибольший коэффициент добротности при прочих равных условиях будет в. том случае, когда вес магнита в два раза больше веса подвижной системы (оси, стрелки, противовесы и т. д.).
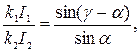
 (2.16)
(2.16) от отношения токов в катушке.
от отношения токов в катушке.


