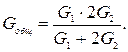Расчет датчика индуктивного манометра
Для расчета электрических параметров датчика необходимо найти индуктивности его катушек, которые определяют через проводимости воздушных зазоров. Точное определение последних представляет большие трудности ввиду трехмерности электромагнитного поля. Расчет произведем аналитическим методом, как наиболее подходящим в данном случае. Для этого магнитное поле в воздушном зазоре и краевое поле выпучивания разбивают на простые фигуры, предварительно находя все геометрические размеры и связывая величины воздушных зазоров с величиной перемещения якоря X.
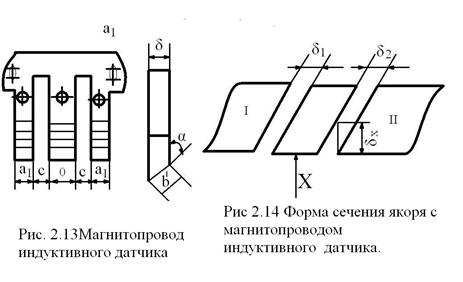
Форма и размеры одного из сердечников магнитной системы показаны на рис. 2.13 и 2.14. Величина перемещения якоря X считается заданной X = 0÷0,6 мм и определяется деформацией мембраны. Воздушный зазор При данной конструкции и размерах магнитной системы, чтобы площадь воздушного зазора между якорем и сердечниками оставалась постоянной, верхний сердечник необходимо поднять на высоту 0,6 мм относительно уровня нижнего сердечника. Задаваясь значениями X от Х=0 до Х=0,6 мм, определяем значения
Для X=0 Так как сердечники имеют одинаковую конструкцию и размеры, достаточно определить проводимости воздушных зазоров между одним из сердечников и якорем. Данные для второго сердечника получаются на основании расчета первого магнитопровода. Магнитный поток проходит не только через воздушный зазор между сердечником и якорем, но и вблизи него, и занимает сложную форму. Объем, по которому замыкается магнитный поток, разбивается на отдельные фигуры, вычисляются их проводимости в отдельности, а затем складываются. Проводимость воздушного зазора под средним стержнем сердечника: 1. Без учета потоков выпучивания
где Дополнительные проводимости, обусловленные потоками выпучивания, определяются по эмпирическим формулам (см. табл. 2.2). Суммарная проводимость среднего сердечника определится как сумма всех найденных проводимостей
Аналогично находим проводимость воздушного зазора под крайним сердечником. Проводимость потоков рассеивания определяется по формуле
где Для определения суммарной магнитной проводимости всей цепи воспользуемся схемой замещения (рис. 2.15), где
G – магнитная проводимость. При построении схемы замещения и при расчете величиной магнитного сопротивления стали Проводимость по этой схеме будет равна
Таблица 2.2
|

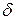 между нижним сердечником и якорем при X = 0 (Р = 0) может браться равным 0,15 мм. Верхний сердечник расположим на таком расстоянии, чтобы при X = 0,6 мм зазор
между нижним сердечником и якорем при X = 0 (Р = 0) может браться равным 0,15 мм. Верхний сердечник расположим на таком расстоянии, чтобы при X = 0,6 мм зазор 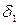 между ним и якорем был равен также 0,15 мм.
между ним и якорем был равен также 0,15 мм. . Как видно из рис. 2.14,
. Как видно из рис. 2.14, 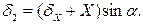
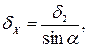 , где
, где  берут равным 45°.
берут равным 45°.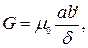
 – магнитная проницаемость воздуха.
– магнитная проницаемость воздуха.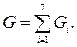
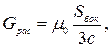
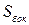 – внутренняя боковая поверхность среднего стержня, занимаемого катушкой.
– внутренняя боковая поверхность среднего стержня, занимаемого катушкой.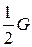 – проводимость воздушного зазора;
– проводимость воздушного зазора;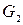 – проводимость железа;
– проводимость железа;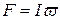 – источник намагничивающей силы;
– источник намагничивающей силы;