Исходные данные для расчета. 2. Конструктивные данные (рис. 2.18).
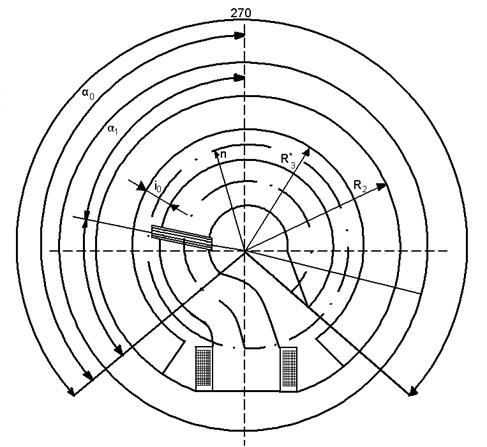
1. Напряжение источника питания 2. Конструктивные данные (рис. 2.18). Число витков рамки Число витков катушки возбуждения Сопротивление рамки Толщина магнитопровода Длина воздушного зазора Радиус средней линии зазора Половина полюсного отклонения подвижной части 3. Экспериментальные данные. Относительная магнитная проницаемость материала магнитопровода Сопротивление потокам рассеяния Комплекс полного электрического сопротивления при начальном положении якоря датчика:
Рис.2.18. Магнитная цепь логометра
Ферродинамический однорамочный логометр переменного тока Ферродинамический логометр является одним из основных узлов указателя и в основном определяет его технические характеристики. Ферродинамический однорамочный логометр представляет собой измерительный механизм, представленный на рис. 2.18, в котором в качестве одного из действующих моментов используется момент, обусловленный изменением индуктивности подвижной рамки при ее повороте, в качестве второго момента — момент, обусловленный изменением взаимной индуктивности. Причем, любой из этих моментов может быть либо вращающим, либо противодействующим. При равенстве этих моментов стрелка устанавливается в положении равновесия, соответствующем измеряемому значению. Для получения достаточно высокого значения этих моментов при большом угле шкалы магнитопровод изготовлен крючкообразной формы.
Рис. 2.19 Распределение магнитных потоков от неподвижной катушки (а) и подвижной рамки (5).
Это обеспечивает достаточно большое изменение индуктивности рамки по углу поворота. При этом величина производной от индуктивности рамки по углу поворота или значение Рассмотрим моменты, действующие в логометре. Причем, для упрощения рассмотрим односекционную катушку возбуждения (рис. 2.19, а). Один из моментов создается, как указывалось выше, взаимодействием тока в рамке
где
и катушки возбуждения; л
Второй момент определяется выражением
где Следовательно, для определения этих моментов необходимо найти зависимость взаимоиндуктивности между рамкой и обмоткой возбуждения от угла поворота Зависимость взаимоиндуктивности
или
где Проводимость
Зависимость индуктивности
Поток
где Откуда
Проводимость Для определения проводимостей выделим поток, проходящий через воздушный зазор, площадь которого определяется углом Ширина элементарного потока равна дуге радиуса Магнитное сопротивление на пути этого потока равно
где
Рис. 2.20. Элементарный поток от подвижной рамки.
Проводимость для элементарного потока
Обозначим
Тогда получим
Проинтегрировав это выражение в пределах от
Аналогично вычислим проводимость слева от рамки
К проводимости
где
Проводимость рассеивания между концами магнитопровода
а проводимость Следовательно, полная проводимость справа от рамки
Полная проводимость слева от рамки
Полная проводимость Тогда
или
Получив выражение для всех проводимостей, можно найти значения взаимоиндуктивности и индуктивности рамки в зависимости от угла отклонения рамки:
Характер изменения
2.21. Характер изменения Мх-р (б) и Lp (а) в зависимости от угла отклонения.
Для дальнейших расчетов необходимо найти Продифференцируем полученные выше выражения для взаимоиндуктивности и индуктивности рамки и подставим их в соответствующие формулы для обоих моментов, предполагая, что при встречающихся параметрах измерительных механизмов знаменатель мало изменяется при изменении угла Поэтому при расчетах считаем его постоянным. Тогда окончательно получим
В момент равновесия
Получена взаимосвязь между углом отклонения рамки и отношением токов в катушке и рамке. Дальнейшие расчеты можно проводить на основании результатов расчета всей измерительной схемы.
|

 частота
частота 
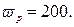




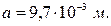
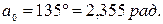
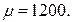
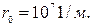
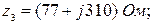


 зависит от положения подвижной рамки.
зависит от положения подвижной рамки.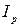 с магнитным потоком в рабочем зазоре я может быть представлен в виде
с магнитным потоком в рабочем зазоре я может быть представлен в виде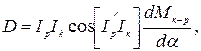
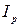 – ток в рамке;
– ток в рамке; – ток в катушке возбуждения;
– ток в катушке возбуждения; – взаимная индуктивность между обмотками рамки
– взаимная индуктивность между обмотками рамки – угол сдвига по фазе между токами рамки и катушки возбуждения;
– угол сдвига по фазе между токами рамки и катушки возбуждения;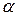 – угол поворота рамки.
– угол поворота рамки.
 – индуктивность рамки.
– индуктивность рамки. сдвига по фазе между токами
сдвига по фазе между токами  и индуктивности рамки как функции угла поворота
и индуктивности рамки как функции угла поворота 
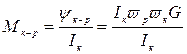
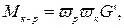
 – поток, создаваемый током
– поток, создаваемый током  и сцепляющийся с подвижной рамкой.
и сцепляющийся с подвижной рамкой. представляет: проводимость справа от рамки
представляет: проводимость справа от рамки  и проводимость рассеяний
и проводимость рассеяний 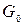 (рис. 2.19), так как определяется частью потока обмоток возбуждения, сцепленного с рамкой:
(рис. 2.19), так как определяется частью потока обмоток возбуждения, сцепленного с рамкой:
 к току
к току 

 – магнитное сопротивление на пути потока рамки.
– магнитное сопротивление на пути потока рамки.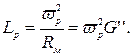
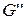 определяется полным сопротивлением потоку
определяется полным сопротивлением потоку 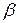 (рис. 2.20).
(рис. 2.20).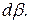 Длина пути прохождения потока равна сумме участков воздушного зазора внешнего и внутреннего сердечников.
Длина пути прохождения потока равна сумме участков воздушного зазора внешнего и внутреннего сердечников.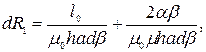
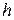 – толщина магнитопровода;
– толщина магнитопровода;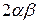 – длина пути потока вдоль внутреннего и внешнего сердечников; принимается приближенно равной
– длина пути потока вдоль внутреннего и внешнего сердечников; принимается приближенно равной  как двойная дуга радиуса
как двойная дуга радиуса  – относительная магнитная проницаемость материала магнитопровода;
– относительная магнитная проницаемость материала магнитопровода;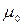 – проницаемость воздуха, равная
– проницаемость воздуха, равная 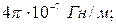
 – длина воздушного зазора.
– длина воздушного зазора.
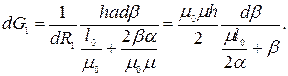

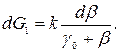
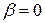 до
до  где
где 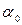 – половина полюсной дуги,
– половина полюсной дуги, 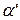 – отклонение рамки от середины полюсной дуги, получим
– отклонение рамки от середины полюсной дуги, получим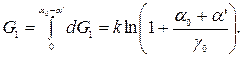
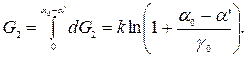
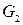 – проводимость стыка
– проводимость стыка 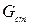 и проводимость рассеивания слева от рамки
и проводимость рассеивания слева от рамки 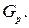 Проводимость стыка можно определить по формуле
Проводимость стыка можно определить по формуле
 – длина средней линии стыка;
– длина средней линии стыка;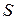 – сечение стыка
– сечение стыка 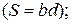
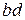 – ширина и толщина стыка.
– ширина и толщина стыка.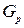 слева от рамки находят расчетным путем с помощью формул, приведенных в работах [6, 13], по расчету магнитных цепей или задаются на основании экспериментальных данных. В данном случае проводимость между концами магнитопровода может быть определена через заданное сопротивление г0 потокам рассеивания
слева от рамки находят расчетным путем с помощью формул, приведенных в работах [6, 13], по расчету магнитных цепей или задаются на основании экспериментальных данных. В данном случае проводимость между концами магнитопровода может быть определена через заданное сопротивление г0 потокам рассеивания
 на 10—20%.
на 10—20%.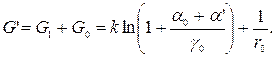

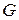 находится при условии, что проводимости слева и справа от рамки включены последовательно.
находится при условии, что проводимости слева и справа от рамки включены последовательно.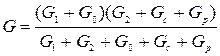




 и построить графики
и построить графики  и
и 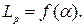

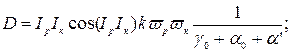


 и тогда имеем
и тогда имеем



