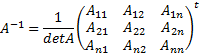Определение определителя. Основные свойства определителя (равноправие строк и столбцов, линейность, кососимметричность определителя).
Определитель – это некоторое число поставленное в соответствие квадратной матрице.
Для неквадратных матриц понятие определителя не вводится.
Свойства:
1) Определитель — кососимметричная полилинейная функция строк (столбцов) матрицы. Полилинейность означает, что определитель линеен по всем строкам (столбцам): 2) При добавлении к любой строке (столбцу) линейной комбинации других строк (столбцов) определитель не изменится. 3) Если две строки (столбца) матрицы совпадают, то её определитель равен нулю. 4) Если две (или несколько) строки (столбца) матрицы линейно зависимы, то её определитель равен нулю. 5) Если переставить две строки (столбца) матрицы, то её определитель умножается на (-1). 6) Общий множитель элементов какого-либо ряда определителя можно вынести за знак определителя. 7) Если хотя бы одна строка (столбец) матрицы нулевая, то определитель равен нулю. 8) Сумма произведений всех элементов любой строки на их алгебраические дополнения равна определителю. 9) Сумма произведений всех элементов любого ряда на алгебраические дополнения соответствующих элементов параллельного ряда равна нулю. 4. Определение алгебраического дополнения. Теорема о разложении определителя по строке. Теорема об определителе произведения двух матриц. Алгебраическим дополнением элемента
где Теорема Лапласа: Пусть
где Утверждение является частным случаем теоремы Лапласа. Достаточно в ней положить Теорема: Определитель произведения двух квадратных матриц А и В одного и того же порядка равен произведению их определителей: det(A*B)=detA*detB 5. Определение обратной матрицы. Свойства обратной матрицы. Критерий обратимости матриц.
Матрица A называется обратимой, если существует такая матрица B, что AB=BA=E. Матрица B называется обратной к A и обозначается Замечание Если матрица А обратима, то из равенства Свойства. Пусть матрица А обратима, тогда 1. уществует единственная матрица обратная к А 2. 3. Если 4. 5. Пусть матрица B так же обратима. Тогда матрица ABобратима и Критерий обратимости. Матрица
|

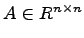
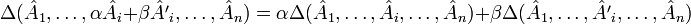 где
где  и т. д. — строчки матрицы,
и т. д. — строчки матрицы, 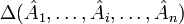 — определитель такой матрицы.
— определитель такой матрицы.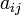 матрицы
матрицы 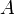 называется число
называется число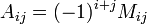 ,
,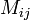 — дополнительный минор, определитель матрицы, получающейся из исходной матрицы
— дополнительный минор, определитель матрицы, получающейся из исходной матрицы 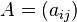 — квадратная матрица размера
— квадратная матрица размера  . Пусть также задан некоторый номер строки
. Пусть также задан некоторый номер строки 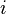 либо номер столбца
либо номер столбца 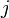 матрицы
матрицы  . Тогда определитель
. Тогда определитель 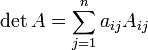 Разложение по
Разложение по 
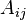 — алгебраическое дополнение к минору, расположенному в строке с номером
— алгебраическое дополнение к минору, расположенному в строке с номером 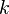 равным 1 и выбрать
равным 1 и выбрать  .
.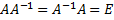 следует, что А квадратная матрица.
следует, что А квадратная матрица. и
и 
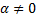 , то
, то 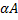 также обратима и
также обратима и 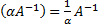
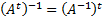

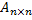 обратима тогда и только тогда, когда
обратима тогда и только тогда, когда