Определение матрицы, операций над матрицами. Свойства операций над матрицами.
Матрицей размера m на n называется совокупность mn вещественных (комплексных) чисел или элементов другой структуры (многочлены, функции и т.д.), записанных в виде прямоугольной таблицы, которая состоит из m строк и n столбцов и взятая в круглые или прямоугольные или в двойные прямые скобки. Операции над матрицами и иx свойства: 1) Сумма двух матриц A и B a. A+B=B+A; (перестановочность или коммутативность операции сложения) b. (A+B)+C = A+(B+C); (ассоциативность или сочетательное свойство) c. A+O = O+A =A; d. A+(-A)=(-A)+A=O. 2) Разность матриц A и B 3) Произведение матрицы A на число a. b. c. d. e. -A=(-1)A. 4) Произведение матриц A и B a. (AB)C=A(BC); (Свойство ассоциативности) b. c. A(B+C)=AB+AC, (A+B)C=AC+BC (Свойство дистрибутивности) 5) Транспонирование матриц A и B a. b. c. d.
|
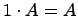
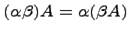
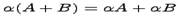(Распределительное свойство относительно сложения матриц);
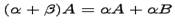(Распределительное свойство относительно сложения чисел);
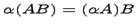(Свойство ассоциативности)
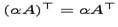для любого действительного числа 
;
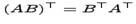
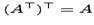для любых матриц A и B, для которых имеют смысл левые части равенств.
