Определения и примеры векторного пространства, векторов, линейной комбинации векторов.Определения и примеры векторного пространства, векторов, линейной комбинации векторов. Непустое множ-во, в кот-ом опред-ны 2 операции: сложение и умножение на число, относит-но кот-х выпол-ны 8 аксиом назыв-ся линейн.вектор. прост-вом. Векторы а1, а2…аm простр-ва Rn наз-ся лин.независ-ми, если урав-е
Имеет единст.нулевое решение λ1=0,…,λk=0 Например, система двух векторов Векторы а1, а2…аm простр-ва Rn наз-ся лин.завис-ми, если найдутся числа λ1,…, λk не равные нулю, для кот-ых выполнено равенство
свойства линейно зависимой системы векторов. 1. Система, состоящая из одного ненулевого вектора, линейно независима. 2. Система, содержащая нулевой вектор, всегда линейно зависима. 3. Система, содержащая более одного вектора, линейно зависима тогда и только тогда, когда среди ее векторов содержится по крайней мере один вектор, который линейно выражается через остальные.
Линейной комбинацией векторов (12.6) называется вектор вида
где λ1, λ2,..., λk — любые действительные числа. Например, пусть даны три вектора: В случае равенства (12.7) говорят также, что вектор
|
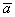1 = (1, 0) и 
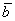= (4, 11, -5).
