Определение характеристического многочлена матрицы, собственного вектора и собственного значения.
Характеристический многочлен матрицы — это многочлен, определяющий её собственные значения. Определение Для данной матрицы Ценность характеристического многочлена в том, что собственные значения матрицы являются его корнями. Действительно, если уравнение Свойства · Для матрицы · Все корни характеристического многочлена матрицы являются её собственными значениями. · Теорема Гамильтона — Кэли: если · Характеристические многочлены подобных матриц совпадают: · Если A и B — две · В более общем виде, если A —
|
, 
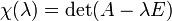, где Е — единичная матрица, является многочленом от 
, который называется характеристическим многочленом матрицы A (иногда также "вековым уравнением" (secular equation)).
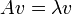имеет не нулевое решение, то 
, значит матрица 
вырождена и ее определитель 
равен нулю.
, характеристический многочлен имеет степень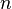 
.
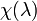— характеристический многочлен матрицы 
.
.
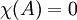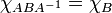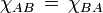. В частности, отсюда вытекает, что tr(AB)=tr(BA) и det(AB)=det(BA).
-матрица, а B —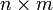 
-матрица, причем m<n, так что AB и BA — квадратные матрицы размеров m и n соответственно, то
.
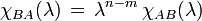