Теорема о связи характеристического многочлена и собственных значениях линейного оператора.
Определение 5. Характеристическим многочленом оператора Теорема 2. Характеристический многочлен линейного оператора Определение 6. Уравнение Предложение 2. Собственное значение Определение 7. Кратность Теорема 3. Геометрическая кратность собственного значения
|

 называется многочлен
называется многочлен  .
. называется характеристическим уравнением оператора
называется характеристическим уравнением оператора 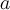 оператора
оператора  . Обратно, любой корень
. Обратно, любой корень 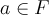 характеристического многочлена является собственным значением оператора
характеристического многочлена является собственным значением оператора  называется алгебраической кратностью собственного значения
называется алгебраической кратностью собственного значения 


