Нормальное уравнение плоскости Расстояние от точки до плоскости . Условия принадлежности 4 точек одной плоскости.В векторной форме уравнение плоскости имеет вид
Если нормальный вектор плоскости – единичный,
тогда уравнение плоскости можно записать в виде
(нормальное уравнение плоскости).
где Общее уравнение плоскости (8) может быть приведено к нормальному виду умножением на нормирующий множитель Расстояние от точки
Пример 16. Даны точки Решение. Вектор
Найдем нормирующий множитель
Умножая уравнение плоскости почленно на нормирующий множитель, получим нормальное уравнение плоскости
где коэффициенты при Ответ: общее уравнение плоскости: Пример 17. Даны точки Решение. Составим уравнение плоскости
Расстояние от
Ответ: расстояние от
|
, 
.
, 
,
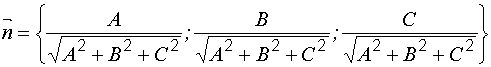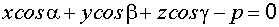
– расстояние от начала координат до плоскости, 
, 
, 
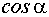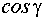– направляющие косинусы нормали
, 
, 
,
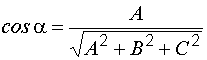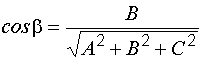– углы между нормалью плоскости и осями координат 
соответственно.
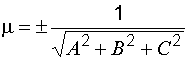, знак перед дробью противоположен знаку свободного члена 
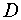в (8).
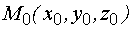до плоскости (8) находится по формуле, полученной подстановкой точки в нормальное уравнение
.
, 
, 
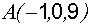. Составить уравнение плоскости, проходящей через 
перпендикулярно вектору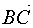 
. Привести его к нормальному виду.
. По формуле (6) составим общее уравнение искомой плоскости
.
.
,
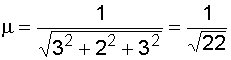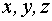– соответствующие направляющие косинусы нормали, расстояние от начала координат до плоскости 
.
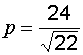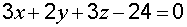; нормальное уравнение: 
, 
, 
. Найти расстояние от точки 
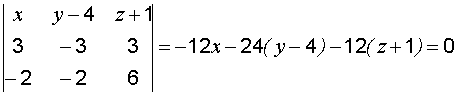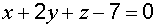до плоскости 
.
,
.
до плоскости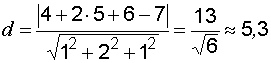 
.
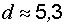ед. длины.
