Швидкість і прискорення
Скалярну величину, яка рівна довжині траєкторії
При прямолінійному русі вектор переміщення співпадає з відповідною ділянкою траєкторії, тобто його модуль рівний пройденому шляху. У випадку криволінійного руху вектор переміщення є січною, що проходить через дві точки траєкторії, які відповідають двом різним моментам часу. Швидкість – це векторна величина, яка характеризує зміну радіуса-вектора рухомої точки з часом. Вектор середньої швидкості рівний відношенню приросту радіуса-вектора
Якщо перейти до границі при
Таким чином,миттєва швидкість – це швидкість в даний момент часу або в даній точці траєкторії. Вектор миттєвої швидкості дорівнює першій похідній радіуса-вектора рухомої точки по часу і напрямлений вздовж дотичної до траєкторії в будь-якій її точці. Врахувавши, що при
В загальному випадку з (1.6) випливає, що шлях може бути обчислений за формулою
Швидкість можна представити через її проекції на координатні вісі
де Швидкість може змінюватись як за модулем так і за напрямком. Для характеристики зміни швидкості вводять вектор прискорення, який описує зміну швидкості з часом. Середнє прискорення рівне відношенню зміни швидкості до проміжку часу, за який вона відбулася
Миттєве прискорення – це прискорення в даний момент часу і воно визначається як границя до якої прямує середнє значення прискорення, якщо проміжок часу прямує до нуля
Таким чином, миттєве прискорення дорівнює першій похідній швидкості по часу або другій похідній радіуса-вектора по часу. В проекціях на координатні вісі
де Коли матеріальна точка рухається по криволінійній траєкторії (рис.1.2), і вектор її швидкості змінюється як за напрямком
Знайдемо миттєве прискорення матеріальної точки, скориставшись формулами (1.12) та (1.16)
та
З рис.1.3 маємо
та
|

 називають шляхом. Вектор, що з’єднує початкове положення матеріальної точки з її положенням в даний момент часу називають вектором переміщення
називають шляхом. Вектор, що з’єднує початкове положення матеріальної точки з її положенням в даний момент часу називають вектором переміщення  .
. . (1.3)
. (1.3)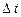 , за який він відбувся
, за який він відбувся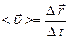 . (1.4)
. (1.4)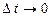 , то отримаємо вираз для миттєвої швидкості
, то отримаємо вираз для миттєвої швидкості . (1.5)
. (1.5) , отримаємо:
, отримаємо: . (1.6)
. (1.6)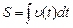 . (1.7)
. (1.7) , (1.8)
, (1.8)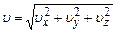 , (1.9)
, (1.9)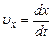 ,
, 
 . (1.10)
. (1.10)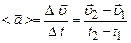 . (1.11)
. (1.11)
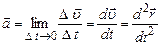 . (1.12)
. (1.12) , (1.13)
, (1.13) , (1.14)
, (1.14)
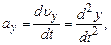
 .(1.15)
.(1.15)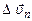 так і за модулем
так і за модулем  , то
, то . (1.16)
. (1.16)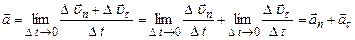 . (1.17)
. (1.17) Отже, повне прискорення рівне сумі нормального
Отже, повне прискорення рівне сумі нормального  і тангенціального
і тангенціального 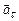 прискорень. Нормальне прискорення характеризує зміну швидкості за напрямком і напрямлене вздовж радіуса до центра кривизни траєкторії. Тангенціальне прискорення характеризує зміну швидкості за модулем і напрямлене вздовж дотичної до траєкторії. Числові значення цих прискорень рівні
прискорень. Нормальне прискорення характеризує зміну швидкості за напрямком і напрямлене вздовж радіуса до центра кривизни траєкторії. Тангенціальне прискорення характеризує зміну швидкості за модулем і напрямлене вздовж дотичної до траєкторії. Числові значення цих прискорень рівні (1.18)
(1.18)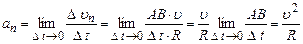 . (1.19)
. (1.19) (1.20)
(1.20)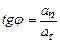 . (1.21)
. (1.21)


