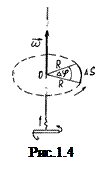
 Нехай матеріальна точка рухається по коловій траєкторії радіусом R з центром в т.0. За час
Нехай матеріальна точка рухається по коловій траєкторії радіусом R з центром в т.0. За час 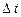 радіус-вектор точки повернеться на деякий кут
радіус-вектор точки повернеться на деякий кут 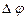 (рис. 1.4). Кутовою швидкістю називають величину, яка є першою похідною кута повороту радіуса-вектора по часу
(рис. 1.4). Кутовою швидкістю називають величину, яка є першою похідною кута повороту радіуса-вектора по часу
 . (1.22)
. (1.22)
Кутова швидкість – це вектор, напрям якого визначається за правилом свердлика.
Крім кутової швидкості, рух тіла по колу ще описують лінійною швидкістю, яка рівна відношенню довжини дуги, що її описує кінець радіуса-вектора, до часу, за який вона пройдена.
 . (1.23)
. (1.23)
Лінійна швидкість напрямлена по дотичній до дуги кола в кожній її точці. При рівномірному русі по колу використовують поняття періода Т та частоти  . Період – це час одного повного оберту, а частота – кількість обертів за одиницю часу. Кутову та лінійну швидкості можна виразити через період або частоту
. Період – це час одного повного оберту, а частота – кількість обертів за одиницю часу. Кутову та лінійну швидкості можна виразити через період або частоту
 (1.24)
(1.24)
та 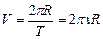 . (1.25)
. (1.25)
Звідси  або
або  . (1.26)
. (1.26)
У векторній формі 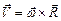 (1.27)
(1.27)
Кутове прискорення  рівне першій похідній кутової швидкості по часу
рівне першій похідній кутової швидкості по часу
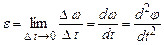 . (1.28)
. (1.28)
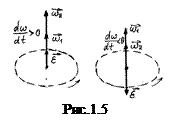
 Вектор кутового прискорення напрямлений вздовж вісі обертання і співпадає з напрямком
Вектор кутового прискорення напрямлений вздовж вісі обертання і співпадає з напрямком 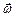 , якщо кутова швидкість зростає, і протилежний до напрямку
, якщо кутова швидкість зростає, і протилежний до напрямку 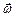 , якщо кутова швидкість зменшується (рис.1.5).
, якщо кутова швидкість зменшується (рис.1.5).
Продиференціювавши вираз (1.27) по t і пам’ятаючи, що матеріальна точка рухається по колу (рис.1.6), тобто  , отримаємо
, отримаємо

Оскільки 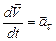 то
то 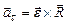 . (1.29)
. (1.29)

 Нехай матеріальна точка рухається по коловій траєкторії радіусом R з центром в т.0. За час
Нехай матеріальна точка рухається по коловій траєкторії радіусом R з центром в т.0. За час 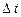 радіус-вектор точки повернеться на деякий кут
радіус-вектор точки повернеться на деякий кут 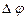 (рис. 1.4). Кутовою швидкістю називають величину, яка є першою похідною кута повороту радіуса-вектора по часу
(рис. 1.4). Кутовою швидкістю називають величину, яка є першою похідною кута повороту радіуса-вектора по часу . (1.22)
. (1.22) . (1.23)
. (1.23) . Період – це час одного повного оберту, а частота – кількість обертів за одиницю часу. Кутову та лінійну швидкості можна виразити через період або частоту
. Період – це час одного повного оберту, а частота – кількість обертів за одиницю часу. Кутову та лінійну швидкості можна виразити через період або частоту (1.24)
(1.24)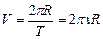 . (1.25)
. (1.25) або
або  . (1.26)
. (1.26)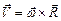 (1.27)
(1.27) рівне першій похідній кутової швидкості по часу
рівне першій похідній кутової швидкості по часу
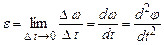 . (1.28)
. (1.28) Вектор кутового прискорення напрямлений вздовж вісі обертання і співпадає з напрямком
Вектор кутового прискорення напрямлений вздовж вісі обертання і співпадає з напрямком 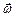 , якщо кутова швидкість зростає, і протилежний до напрямку
, якщо кутова швидкість зростає, і протилежний до напрямку  , отримаємо
, отримаємо
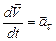 то
то 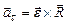 . (1.29)
. (1.29)


