Правила додавання швидкостей в релятивістській механіці
Спираючись на перетворення Лоренца, знайдемо зв’язок між швидкостями тіла в двох інерціальних системах відліку ( За означенням швидкості Продиференціюємо перше і четверте рівняння перетворень Лоренца
Поділимо почленно ліві і праві частини отриманих рівнянь
Замінивши похідні відповідними компонентами швидкості, дістанемо
Отже, Отримані формули виражають правило додавання швидкостей в релятивістській механіці. Нехай
Бачимо, що результуюча швидкість
|
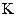і 
). Розглянемо простий випадок, коли тіло рухається паралельно до осі 
(або 
). Тоді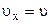 
; 
; 
, відповідно 
; 
; 
.
, 
.
; 
.
.
.
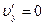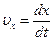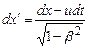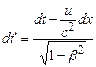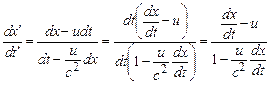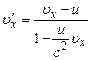або 
.
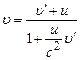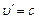і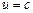 
. Тоді
.
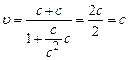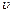не перевищує швидкості світла у вакуумі. Отже, швидкість світла у вакуумі є граничною швидкістю. І ніякі дослідні факти в сучасній фізиці не заперечують висновку про те, що швидкість світла у вакуумі є межею можливих швидкостей в природі.
