Постулати спеціальної теорії відносності (СТВ). Перетворення Лоренца
1. Швидкість світла і правило додавання швидкостей. До середини XIX ст. швидкість світла була виміряна вже досить точно. Її значення у вакуумі складає 3·108м/с. Виникло питання про те, до якої інерціальної системи відноситься це значення швидкості. І виникло воно тому, що згідно з правилом додавання швидкостей у класичній фізиці
швидкість руху, в тому числі і швидкість руху світла, в різних інерціальних системах відліку різна. Експериментальні ж дослідження в цьому напрямі показали, що швидкість руху світла в різних інерціальних системах відліку однакова, що суперечить (1.82). Отже, перетворення Галілея, з яких слідує правило (1.82), мають обмежену область застосування; вони застосовні, коли І так виникла необхідність переглянути ті основні положення, які лежать в основі перетворень Галілея, зокрема положення про абсолютність простору і часу. Цю задачу в 1905 році розв’язав Ейнштейн. 2. Постулати СТВ. В основі теорії Ейнштейна лежать два положення, які називають постулатами спеціальної теорії відносності: 1). В усіх інерціальних системах відліку всі фізичні явища (механічні, електричні, магнітні, оптичні) при одних і тих же умовах протікають однаково (принцип відносності). 2). Швидкість світла у вакуумі однакова в усіх інерціальних системах відліку і не залежить від руху джерела світла (принцип інваріантності швидкості світла). 3. Перетворення Лоренца. Виходячи з цих положень Ейнштейн показав, що зв’язок між координатами і часом у двох інерціональних системах відліку ( У випадку, коли координатні осі
де Звернемо увагу на першу і останню формули. Вони наочно вказують на те, що не тільки координата залежить від часу, але й час залежить від координати, тобто між простором і часом є взаємозв’язок. Координата і час залежать також від швидкості системи відліку, тобто властивості простору і часу залежать від характеру руху матеріальних об’єктів – простір і час є якостями існування матерії. Дуже істотно, що при
§ 1.24. Властивості простору і часу в релятивістській механіці (наслідки із перетворень Лоренца) 1. Поняття одночасності подій. Нехай у системі Якщо події в системі
тобто ці події є одночасними і такими, що просторово збігаються для довільної інерціальної системи відліку. Якщо події в системі
Бачимо, що
Отже, в системі 2. Відносність довжини. Нехай деяке тіло (наприклад, стрижень), розміщене вздовж осі За першою формулою перетворень Лоренца маємо
Оскільки Отже, довжина стрижня, виміряна в системі, відносно якої він рухається, є меншою від довжини, виміряної в системі, відносно якої стрижень знаходиться у стані спокою. Лінійні розміри стрижня в системі відліку, відносно якої він не рухається, є найбільшими. Ці найбільші розміри називають власними розмірами. Зауважимо, що твердження про скорочення лінійних розмірів тіл у напрямі руху не означає якогось фізичного процесу в стрижні, подібного деформації. 3. Відносність проміжку часу. Нехай у деякій точці, яка нерухома в системі
За четвертою формулою перетворень Лоренца маємо
Тривалість події в системі Тоді
Оскільки Отже, проміжок часу між двома подіями в різних інерціальних системах відліку різний; проміжок часу відносний. Він найменший в тій системі відліку, відносно якої точка, де відбувається подія, нерухома. Цей найменший проміжок часу називається власним часом. Формула (1.83) знайшла своє експериментальне підтвердження. В космічних променях є такі елементарні частинки як 4. Поняття інтервалу між двома подіями. З назви теорії і її попередніх результатів може скластися хибна думка про те, що “все в світі відносне”. Насправді, теорія відносності точніше, ніж класична фізика, відображує поняття абсолютного і відносного в розвитку матеріального світу та його пізнанні. З приводу СТВ Планк у свій час писав: “Її привабливість для мене полягає в тому, що я прагнув з усіх її положень вивести те абсолютне, інваріантне, що лежить в її основі”. І такі абсолютні, інваріантні величини були знайдені. Взаємозв’язок між простором і часом показує, що для математичного відображення будь-якої події слід користуватися чотиривимірною системою відліку, де роль четвертої координати відіграє час. Точку в такій системі відліку, яка визначає певну подію, називають світовою точкою. Розглянемо дві події. Нехай в системі відліку одна з них визначається координатами Величину Неважко показати, що інтервал є інваріантом відносно перетворень Лоренца. Квадрат інтервалу в системі
а відповідний квадрат інтервалу між двома подіями в системі
Використавши формули
та підставивши їх у вираз (1.84), дістанемо Інтервал між подіями можна виразити через такі дві компоненти: квадрат просторової відстані
та квадрат проміжку часу
Тоді
З виразу (6.4) видно, що хоч обидві компоненти мають відносний характер, інтервал, як і швидкість світла, інваріантні відносно перетворень Лоренца. Останні в теорії відносності належать до абсолютних величин.
|

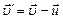 , (1.82)
, (1.82) .
.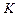 і
і  ) виражається не перетвореннями Галілея, а перетвореннями Лоренца.
) виражається не перетвореннями Галілея, а перетвореннями Лоренца.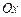 і
і 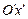 систем відліку
систем відліку 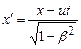 ;
; 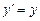 ;
; 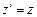 ;
; 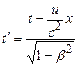 ,
,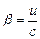 (
(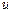 – відносна швидкість систем відліку;
– відносна швидкість систем відліку; 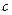 швидкість світла у вакуумі).
швидкість світла у вакуумі).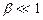 формули Лоренца переходять у формули перетворень Галілея(1.72), у згоді з Принципом відповідності: попередня теорія є граничним випадком більш загальної теорії, і тоді їх результати співпадають.
формули Лоренца переходять у формули перетворень Галілея(1.72), у згоді з Принципом відповідності: попередня теорія є граничним випадком більш загальної теорії, і тоді їх результати співпадають.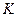 в точках з координатами
в точках з координатами 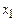 і
і 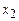 в моменти часу
в моменти часу 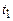 і
і 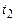 відбуваються дві події. В системі
відбуваються дві події. В системі 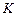 з швидкістю
з швидкістю 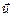 вздовж осі
вздовж осі 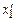 і
і 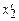 в моменти часу
в моменти часу 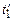 і
і 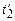 .
.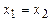 ) і є одночасними (
) і є одночасними (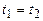 ), то згідно з перетвореннями Лоренца
), то згідно з перетвореннями Лоренца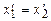 і
і 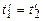 ,
,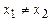 ), але одночасні (
), але одночасні (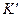
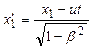 ;
; 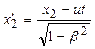 ,
,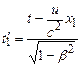 ;
; 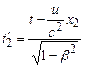 .
.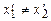 і
і 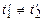 .
.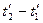 визначається знаком виразу
визначається знаком виразу 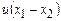 , тому в різних точках системи
, тому в різних точках системи 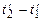 буде неоднаковою за величиною і за знаком.
буде неоднаковою за величиною і за знаком.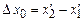 , де
, де 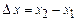 .
.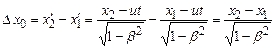 .
.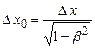 або
або 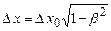 .
.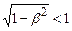 , то
, то 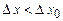 .
.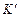 , відбувається подія, тривалість якої
, відбувається подія, тривалість якої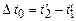 .
.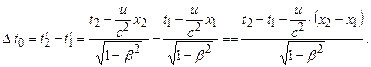

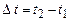 , а різниця
, а різниця 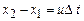 – зміщення точки, де відбувається подія, в системі
– зміщення точки, де відбувається подія, в системі 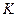 .
.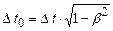 або
або 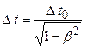 . (1.83)
. (1.83)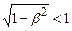 , то
, то 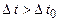 .
.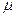 – мезони. Ці частинки нестабільні – вони перетворюються на інші елементарні частинки. Час життя
– мезони. Ці частинки нестабільні – вони перетворюються на інші елементарні частинки. Час життя  – мезонів, коли вони знаходяться у стані спокою, складає
– мезонів, коли вони знаходяться у стані спокою, складає 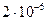 с. За такий час, навіть рухаючись зі швидкістю світла,
с. За такий час, навіть рухаючись зі швидкістю світла, 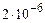 с. це власний час життя мезонів, тобто час виміряний по годиннику, який рухається разом з частинкою. Час виміряний по годиннику в системі відліку, зв’язаною із Землею більший і частинка встигає пролетіти більшу відстань.
с. це власний час життя мезонів, тобто час виміряний по годиннику, який рухається разом з частинкою. Час виміряний по годиннику в системі відліку, зв’язаною із Землею більший і частинка встигає пролетіти більшу відстань.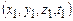 , а друга – координатами
, а друга – координатами 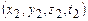 .
.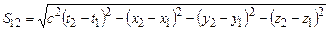 називають інтервалом між двома подіями.
називають інтервалом між двома подіями.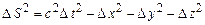 ,
,
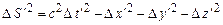 . (1.84)
. (1.84)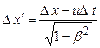 ;
; 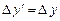 ;
; 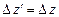 ;
; 
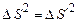 .
.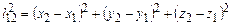
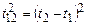 .
.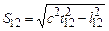 . (1.85)
. (1.85)


