Конденсатори. Електроємність конденсатора. З’єднання конденсаторів
Здатність провідника накопичувати електричний заряд характеризується його електроємністю, вона пропорційна до розмірів провідника. Однак електроємність навіть великого за розміром провідника є малою і недостатньою для практичного використання. Розглянемо систему двох провідників розділених діелектриком, яку будемо називати конденсатором. Зарядимо кожен із провідників рівними за величиною і протилежними за знаком зарядами. Це рівнозначно перенесенню деякого електричного заряду з одного провідника (обкладки конденсатора) на інший. Внаслідок взаємного притягання між протилежними за знаком зарядами обкладок конденсатора кожен із провідників конденсатора має значно більшу накопичувальну здатність, ніж відокремлений провідник. Тому електроємність конденсатора є значно більшою, ніж електроємність відокремленого провідника. Електроємністю конденсатора називається фізична величина, рівна зарядові, який необхідно перенести з однієї обкладки на іншу, щоб різниця потенціалів між ними змінилась на одиницю
де За формою обкладок конденсатори поділяють на плоскі, циліндричні і сферичні.
Напруженість електричного поля між обкладками рівна
де
Різницю потенціалів знайдемо за формулою (3.73)
Підставляючи (3.102) в (3.99), одержимо формулу електроємності плоского конденсатора
Напруженості електричного поля ззовні від конденсатора, створеного однією та іншою обкладками, взаємно компенсуються. Тому результуюча напруженість електричного поля ззовні від конденсатора рівна нулю.
Напруженість електричного поля всередині внутрішнього циліндра рівна нулю, оскільки електричне поле всередині провідника відсутнє. Напруженість електричного поля в просторі між циліндрами створюється лише зарядом внутрішнього циліндра і рівна Напруженість електричного поля ззовні від циліндра радіусом Різницю потенціалів між обома циліндрами знайдемо за формулою (3.89)
де
Підставимо (3.105) в (3.104)
Підставимо (3.106) у формулу (3.99) і одержимо формулу електроємності циліндричного конденсатора
Напруженість електричного поля всередині внутрішнього сферичного провідника рівна нулю. Напруженість електричного поля в просторі між сферичними провідниками створюється лише зарядом внутрішньої кулі і рівна Напруженість електричного поля ззовні від сферичного провідника радіусом Різницю потенціалів між обома сферичними провідниками знайдемо за формулою (3.88)
Підставимо (3.108) у формулу (3.99) і одержимо формулу електроємності сферичного конденсатора
Для практичних потреб конденсатори часто з’єднують між собою в батареї. Найбільш поширеними є паралельне і послідовне з’єднання конденсаторів. Розглянемо паралельне з’єднання конденсаторів при якому позитивно заряджені обкладки всіх конденсаторів з’єднують в один полюс, а негативно заряджені обкладки – в інший полюс (рис.3.22). При паралельному з’єднанні конденсаторів напруга на всіх конденсаторах однакова, а заряд батареї конденсаторів рівний серії зарядів на кожному з них
Підставивши (3.110) і (3.111) у формулу (3.99), одержимо формулу електроємності при паралельному з’єднанні конденсаторів
При послідовному з’єднанні конденсаторів заряди всіх конденсаторів однакові, а напруга батареї конденсаторів рівна сумі напруг на кожному із них
Підставивши (3.113) і (3.114) у формулу (3.99), одержимо формулу електроємності при послідовному з’єднанні конденсаторів
|

 , (3.99)
, (3.99)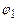 і
і 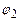 – потенціали обкладок,
– потенціали обкладок, 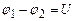 – різниця потенціалів.
– різниця потенціалів. Розглянемо плоский конденсатор, який складається з двох плоских паралельних обкладок площею
Розглянемо плоский конденсатор, який складається з двох плоских паралельних обкладок площею  кожна, які знаходяться на відстані
кожна, які знаходяться на відстані 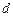 одна від одної (рис. 3.19). Нехай між обкладками міститься діелектрик з діелектричною проникністю
одна від одної (рис. 3.19). Нехай між обкладками міститься діелектрик з діелектричною проникністю  і обкладки заряджені зарядами
і обкладки заряджені зарядами 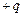 і
і 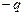 .
.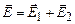 , (3.100)
, (3.100)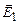 і
і  – напруженості полів, створених кожною з обкладинок. Будемо вважати розміри обкладок конденсатора значно більшими ніж відстань між ними. Тоді величини
– напруженості полів, створених кожною з обкладинок. Будемо вважати розміри обкладок конденсатора значно більшими ніж відстань між ними. Тоді величини  і
і 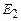 можемо визначити за формулою (3.55) напруженості електричного поля створеного нескінченою рівномірно зарядженою площиною
можемо визначити за формулою (3.55) напруженості електричного поля створеного нескінченою рівномірно зарядженою площиною . (3.101)
. (3.101) . (3.102)
. (3.102)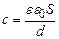 . (3.103)
. (3.103) Розглянемо циліндричний конденсатор, який складається з двох коаксіальних циліндричних провідників з радіусами
Розглянемо циліндричний конденсатор, який складається з двох коаксіальних циліндричних провідників з радіусами  і
і 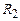 , які вставлені один в одний. Нехай між циліндрами міститься діелектрик з діелектричною проникністю
, які вставлені один в одний. Нехай між циліндрами міститься діелектрик з діелектричною проникністю  . Зовнішній циліндр тут електричного поля не створює, оскільки цей простір для нього є внутрішнім.
. Зовнішній циліндр тут електричного поля не створює, оскільки цей простір для нього є внутрішнім. , (3.104)
, (3.104)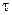 – лінійна густина заряду
– лінійна густина заряду . (3.105)
. (3.105)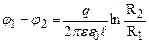 . (3.106)
. (3.106)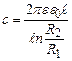 . (3.107)
. (3.107) (рис. 3.21).
(рис. 3.21).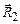 рівна нулю, оскільки тут електричні поля від обох заряджених сферичних провідників взаємно компенсуються.
рівна нулю, оскільки тут електричні поля від обох заряджених сферичних провідників взаємно компенсуються.
 . 3.108)
. 3.108)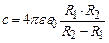 . (3.109)
. (3.109)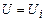 . (3.110)
. (3.110)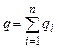 . (3.111)
. (3.111)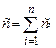 . (3.112)
. (3.112) . (3.113)
. (3.113)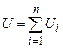 . (3.114)
. (3.114) . (3.115)
. (3.115)


