Енергія зарядженого тіла і конденсатора. Енергія і густина енергії електричного поля
Розглянемо відокремлений провідник з електроємністю
Перенесемо з нескінченності, де потенціал рівний нулю, елементарний заряд
Між однойменними електричними зарядами Зміна потенціальної енергії рівна виконаній роботі з протилежним знаком, тобто
Підставивши (3.116) в (3.118) і проінтегрувавши, дістанемо формулу енергії зарядженого провідника
де С – постійна інтегрування. Будемо вважати, що енергія незарядженого провідника рівна нулю
Підставимо умови (3.120) у вираз (3.119) і визначимо постійну інтегрування С
Підставимо (3.121) у формулу (3.119) і одержимо формулу потенціальної енергії зарядженого провідника
Використовуючи формулу (3.116) можна отримати інші формули для енергії зарядженого провідника:
Розглянемо конденсатор з електроємністю с, якому наданий електричний заряд q. Напруга між обкладками конденсатора рівна
Перенесемо з однієї обкладки на іншу елементарний заряд dq. При цьому електричним полем буде виконана від’ємна робота, оскільки переміщення заряду dq здійснюється проти сили електричного поля
Зміна потенціальної енергії конденсатора рівна виконаній роботі з протилежним знаком, тому вона рівна
Проінтегруємо (3.126) і використовуючи формулу (3.124) отримаємо формули енергії зарядженого конденсатора
Знайдемо енергію зарядженого плоского конденсатора. Підставимо вираз для електроємності плоского конденсатора (3.103) у формулу (3.127)
Введемо позначення
де
Враховуючи зв’язок між напруженістю та індукцією електричного поля (3.7) формулу (3.130) можна представити також у вигляді
Формули (3.130) і (3.131) виражають енергію зарядженого плоского конденсатора через такі характеристики електричного поля як напруженість та індукція, а також через об’єм простору в якому локалізоване електричне поле. Тому можна зробити висновок, що електричне поле володіє енергією. Густиною енергії електричного поля називається фізична величина рівна енергії електричного поля в одиниці об’єму простору де міститься електричне поле
Якщо електричне поле однорідне, то густину енергії електричного поля можна визначити за формулою
Підставимо вирази (3.130) і (3.131) у формулу (3.133). отримаємо формули густини енергії електричного поля
Із формули (3.132) визначимо диференціал енергії електричного поля
Підставимо (3.134) в (3.135)
Проінтегруємо вираз (3.136) по деякому об’єму
Ці формули дозволяють визначити енергію неоднорідного електричного поля.
|

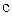 і електричним зарядом
і електричним зарядом 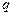 . Потенціал провідника рівний
. Потенціал провідника рівний . (3.116)
. (3.116)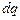 на поверхню провідника. При цьому електричним полем буде виконана робота
на поверхню провідника. При цьому електричним полем буде виконана робота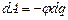 . (3.117)
. (3.117)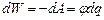 . (3.118)
. (3.118)
 , (3.119)
, (3.119) ;
; 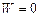 . (3.120)
. (3.120) . (3.121)
. (3.121) . (3.122)
. (3.122) ;
; 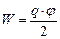 . (3.123)
. (3.123) . (3.124)
. (3.124)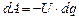 . (3.125)
. (3.125)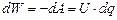 . (3.126)
. (3.126)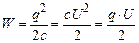 . (3.127)
. (3.127) . (3.128)
. (3.128)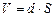 , (3.129)
, (3.129) – об’єм простору між обкладками плоского конденсатора. Підставимо (3.129) і вираз (3.101) напруженості електричного поля всередині плоского конденсатора у формулу (3.128) і одержимо
– об’єм простору між обкладками плоского конденсатора. Підставимо (3.129) і вираз (3.101) напруженості електричного поля всередині плоского конденсатора у формулу (3.128) і одержимо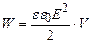 . (3.130)
. (3.130)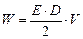 . (3.131)
. (3.131)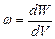 . (3.132)
. (3.132)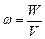 . (3.133)
. (3.133) . (3.134)
. (3.134) . (3.135)
. (3.135)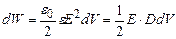 . (3.136)
. (3.136) . (3.137)
. (3.137)


