Провідниками називаються тіла, які мають вільні електричні заряди, тобто такі заряджені частинки, які можуть вільно переміщатись по об’єму провідника. Розглянемо для прикладу металевий провідник, в якому вільними зарядами є електрони. Кожен електрон має негативний електричний заряд, модуль якого рівний елементарному зарядові.
Вмістимо провідник в електричне поле. На рис. 3.18 провідник вміщений в однорідне зовнішнє електричне поле. Під дією зовнішнього поля з напруженістю  електрони в провіднику будуть переміщатись в напрямку, протилежному до напрямку поля
електрони в провіднику будуть переміщатись в напрямку, протилежному до напрямку поля  , внаслідок чого в провіднику виникне внутрішнє електричне поле
, внаслідок чого в провіднику виникне внутрішнє електричне поле  , протилежне за напрямком до зовнішнього. Переміщення електронів буде продовжуватись до тих пір, поки внутрішнє поле повністю не зкомпенсує зовнішнє. При цьому напруженість результуючого електричного поля всередині провідника стане рівною нулеві. Таким чином, зовнішнє електричне поле не може проникнути всередину провідника. Тобто електричне поле всередині провідника завжди відсутнє. Це стосується і того випадку, коли всередині провідника є порожнини.
, протилежне за напрямком до зовнішнього. Переміщення електронів буде продовжуватись до тих пір, поки внутрішнє поле повністю не зкомпенсує зовнішнє. При цьому напруженість результуючого електричного поля всередині провідника стане рівною нулеві. Таким чином, зовнішнє електричне поле не може проникнути всередину провідника. Тобто електричне поле всередині провідника завжди відсутнє. Це стосується і того випадку, коли всередині провідника є порожнини.
Явище виникнення в провіднику внутрішнього електричного поля, рівного за величиною і протилежного за напрямком до зовнішнього, називається електростатичною індукцією. Це явище використовується для захисту електричних приладів та інших об’єктів від впливу зовнішнього електричного поля. З цією метою електричний прилад вміщують в замкнену металеву оболонку, яку, як правило, заземлюють. Такий метод захисту називається електростатичним захистом.
Слід зазначити, що явище електростатичної індукції в повній мірі стосується лише постійного, тобто статичного електричного поля. Змінне електричне поле частково може проникати вглиб провідника.
На основі формули (3.82) можна встановити зв’язок між потенціалом  і напруженістю
і напруженістю  електричного поля
електричного поля

Оскільки всередині провідника  , то
, то  , а отже
, а отже 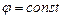 .
.
 Таким чином, потенціал електричного поля всередині провідника і на його поверхні є постійною величиною, а сама поверхня провідника є еквіпотенціальною. Силові лінії електричного поля завжди перпендикулярні до еквіпотенціальних поверхонь. Внаслідок цього силові лінії зовнішнього електричного поля біля провідника викривляються таким чином, що стають перпендикулярними до поверхні провідника як зображено на рис. 3.18. Ця властивість провідників використовується для створення електричних полів потрібної конфігурації за допомогою провідників спеціальної форми в електронних лампах, електронно-променевих трубках, електронних мікроскопах. В цих електронних приладах за допомогою провідників спеціальної форми (електродів) створюють елементи електронної оптики – електронні лінзи, дзеркала, призми.
Таким чином, потенціал електричного поля всередині провідника і на його поверхні є постійною величиною, а сама поверхня провідника є еквіпотенціальною. Силові лінії електричного поля завжди перпендикулярні до еквіпотенціальних поверхонь. Внаслідок цього силові лінії зовнішнього електричного поля біля провідника викривляються таким чином, що стають перпендикулярними до поверхні провідника як зображено на рис. 3.18. Ця властивість провідників використовується для створення електричних полів потрібної конфігурації за допомогою провідників спеціальної форми в електронних лампах, електронно-променевих трубках, електронних мікроскопах. В цих електронних приладах за допомогою провідників спеціальної форми (електродів) створюють елементи електронної оптики – електронні лінзи, дзеркала, призми.
Надамо деякому відокремленому провідникові заряду 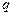 . Цей заряд розподілиться по поверхні провідника таким чином, що потенціал всіх точок поверхні і об’єму стане рівним
. Цей заряд розподілиться по поверхні провідника таким чином, що потенціал всіх точок поверхні і об’єму стане рівним  . Напруженість електричного поля всередині провідника дорівнюватиме нулеві. Експериментально встановлено, що між величиною електричного заряду
. Напруженість електричного поля всередині провідника дорівнюватиме нулеві. Експериментально встановлено, що між величиною електричного заряду  і потенціалом поверхні провідника
і потенціалом поверхні провідника  існує пряма пропорційна залежність
існує пряма пропорційна залежність
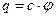 . (3.95)
. (3.95)
Величина  називається електричною ємністю провідника або електроємністю.
називається електричною ємністю провідника або електроємністю.
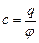 . (3.96)
. (3.96)
Електроємністю відокремленого провідника називається фізична величина рівна зарядові, який необхідно надати провідникові, щоб змінити його потенціал на одиницю. Електроємність залежить від форми, розмірів провідника, діелектричної проникності оточуючого середовища і не залежить від матеріалу провідника, його агрегатного стану, наявності в провіднику порожнин.
Одиницею вимірювання електроємності в системі одиниць  є 1Фарад. 1Фарад – це електроємність такого провідника, потенціал якого змінюється на 1В при зміні його заряду на 1Кл.
є 1Фарад. 1Фарад – це електроємність такого провідника, потенціал якого змінюється на 1В при зміні його заряду на 1Кл.
Визначимо електроємність провідника у формі кулі радіусом 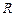 . Надамо йому електричного заряду
. Надамо йому електричного заряду 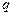 . Приймемо у формулі (3.88) що для поверхні кулі
. Приймемо у формулі (3.88) що для поверхні кулі 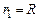 і
і 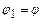 , а для іншої точки, яку віддалимо на нескінченно велику відстань (
, а для іншої точки, яку віддалимо на нескінченно велику відстань (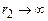 ), потенціал приймемо рівним нулеві
), потенціал приймемо рівним нулеві 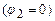 . Таким чином, із виразу (3.88) отримаємо формулу потенціалу поверхні зарядженої кулі.
. Таким чином, із виразу (3.88) отримаємо формулу потенціалу поверхні зарядженої кулі.
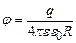 . (3.97)
. (3.97)
Підставимо (3.97) у формулу (3.96) і отримаємо формулу електроємності кулі
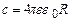 . (3.98)
. (3.98)

 електрони в провіднику будуть переміщатись в напрямку, протилежному до напрямку поля
електрони в провіднику будуть переміщатись в напрямку, протилежному до напрямку поля  , протилежне за напрямком до зовнішнього. Переміщення електронів буде продовжуватись до тих пір, поки внутрішнє поле повністю не зкомпенсує зовнішнє. При цьому напруженість результуючого електричного поля всередині провідника стане рівною нулеві. Таким чином, зовнішнє електричне поле не може проникнути всередину провідника. Тобто електричне поле всередині провідника завжди відсутнє. Це стосується і того випадку, коли всередині провідника є порожнини.
, протилежне за напрямком до зовнішнього. Переміщення електронів буде продовжуватись до тих пір, поки внутрішнє поле повністю не зкомпенсує зовнішнє. При цьому напруженість результуючого електричного поля всередині провідника стане рівною нулеві. Таким чином, зовнішнє електричне поле не може проникнути всередину провідника. Тобто електричне поле всередині провідника завжди відсутнє. Це стосується і того випадку, коли всередині провідника є порожнини. і напруженістю
і напруженістю 
 , то
, то  , а отже
, а отже 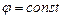 .
. Таким чином, потенціал електричного поля всередині провідника і на його поверхні є постійною величиною, а сама поверхня провідника є еквіпотенціальною. Силові лінії електричного поля завжди перпендикулярні до еквіпотенціальних поверхонь. Внаслідок цього силові лінії зовнішнього електричного поля біля провідника викривляються таким чином, що стають перпендикулярними до поверхні провідника як зображено на рис. 3.18. Ця властивість провідників використовується для створення електричних полів потрібної конфігурації за допомогою провідників спеціальної форми в електронних лампах, електронно-променевих трубках, електронних мікроскопах. В цих електронних приладах за допомогою провідників спеціальної форми (електродів) створюють елементи електронної оптики – електронні лінзи, дзеркала, призми.
Таким чином, потенціал електричного поля всередині провідника і на його поверхні є постійною величиною, а сама поверхня провідника є еквіпотенціальною. Силові лінії електричного поля завжди перпендикулярні до еквіпотенціальних поверхонь. Внаслідок цього силові лінії зовнішнього електричного поля біля провідника викривляються таким чином, що стають перпендикулярними до поверхні провідника як зображено на рис. 3.18. Ця властивість провідників використовується для створення електричних полів потрібної конфігурації за допомогою провідників спеціальної форми в електронних лампах, електронно-променевих трубках, електронних мікроскопах. В цих електронних приладах за допомогою провідників спеціальної форми (електродів) створюють елементи електронної оптики – електронні лінзи, дзеркала, призми.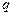 . Цей заряд розподілиться по поверхні провідника таким чином, що потенціал всіх точок поверхні і об’єму стане рівним
. Цей заряд розподілиться по поверхні провідника таким чином, що потенціал всіх точок поверхні і об’єму стане рівним  і потенціалом поверхні провідника
і потенціалом поверхні провідника 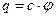 . (3.95)
. (3.95) називається електричною ємністю провідника або електроємністю.
називається електричною ємністю провідника або електроємністю.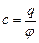 . (3.96)
. (3.96) є 1Фарад. 1Фарад – це електроємність такого провідника, потенціал якого змінюється на 1В при зміні його заряду на 1Кл.
є 1Фарад. 1Фарад – це електроємність такого провідника, потенціал якого змінюється на 1В при зміні його заряду на 1Кл.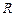 . Надамо йому електричного заряду
. Надамо йому електричного заряду 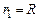 і
і 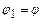 , а для іншої точки, яку віддалимо на нескінченно велику відстань (
, а для іншої точки, яку віддалимо на нескінченно велику відстань (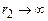 ), потенціал приймемо рівним нулеві
), потенціал приймемо рівним нулеві 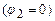 . Таким чином, із виразу (3.88) отримаємо формулу потенціалу поверхні зарядженої кулі.
. Таким чином, із виразу (3.88) отримаємо формулу потенціалу поверхні зарядженої кулі.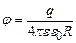 . (3.97)
. (3.97)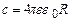 . (3.98)
. (3.98)


