Робота сил електричного поля. Теорема про циркуляцію вектора напруженості електричного поля. Потенціал
Запишемо формулу напруженості електричного поля
Визначимо з цієї формули силу
Підставимо вираз (3.58) у формулу (3.56)
або
Проінтегрувавши вираз (3.59), одержимо формулу роботи при переміщенні електричного заряду
Нехай точковий електричний заряд
З рисунка одержимо
Підставимо (3.62) і (3.63) у вираз (3.60)
Проінтегруємо цей вираз
Отже робота сил електричного поля не залежить від форми траєкторії, а залежить лише від положення початкової і кінцевої точки. Тому електростатичне поле є потенціальним. При переміщенні електричного заряду
Інтеграл по замкнутому контуру Робота потенціальних сил рівна зміні потенціальної енергії з протилежним знаком
З порівняння формул (3.64) і (3.65) можна одержати формулу потенціальної енергії взаємодії двох точкових зарядів:
Для характеристики потенціального поля можна використати поняття потенціалу.
Одиницею вимірювання потенціалу в системі одиниць Підставивши вираз (3.67) в (3.68) отримаємо формулу потенціалу точкового заряду
На рис.3.11.зображено залежність потенціалу точкового електричного заряду від відстані графічно. Продиференціюємо вираз (3.68)
Оскільки
Підставимо (3.59) в (3.71), отримаємо:
Проінтегруємо вираз (3.72) вздовж кривої
Формула (3.73) визначає зв’язок між різницею потенціалів і напруженістю електричного поля. Підставимо вираз (3.73) у формулу (3.61). Отримаємо зв’язок між роботою при переміщенні електричного заряду
Нехай точковий електричний заряд
де Із формули (3.75) одержимо
Якщо потенціал електричного поля
подібні формули можна отримати і при переміщенні заряду вздовж осей координат
Виразимо вектор напруженості електричного поля
де Підставимо (3.76), (3.77) і (3.78) у формулу(3.79)
Формула (3.80) визначає зв’язок між напруженістю електричного поля і потенціалом. Цю формулу можна представити в більш компактному вигляді використовуючи поняття векторного диференціального оператора градієнт
Використовуючи (3.81) формулу (3.80) можна представити у вигляді
Нехай точковий електричний заряд
Поділимо рівність (3.83) на
Використовуючи означення потенціалу (3.68) формулу (3.83) можна записати у вигляді
Для графічного зображення електричних полів поряд із силовими лініями використовуються еквіпотенціальні поверхні. Еквіпотенціальною поверхнеюназивається така поверхня, в кожній точці якої потенціал електричного поля має однакове значення. Тобто еквіпотенціальна поверхня - це поверхня однакового потенціалу. Силові лінії електричного поля перпендикулярні до еквіпотенціальних поверхонь. На рис.3.12 зображено силові лінії та еквіпотенціальні поверхні точкового позитивного заряду.
|

 Нехай електричний заряд
Нехай електричний заряд 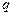 здійснює елементарне переміщення
здійснює елементарне переміщення 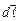 під дією сили
під дією сили 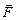 електричного поля напруженістю
електричного поля напруженістю  , як зображено на рис. 3.10. Тоді виконана полем елементарна робота рівна
, як зображено на рис. 3.10. Тоді виконана полем елементарна робота рівна . (3.56)
. (3.56) . (3.57)
. (3.57)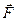
 . (3.58)
. (3.58)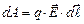 , (3.59)
, (3.59)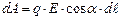 . (3.60)
. (3.60)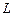
 . (3.61)
. (3.61) , тоді модуль напруженості електричного поля створеного зарядом
, тоді модуль напруженості електричного поля створеного зарядом 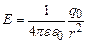 . (3.62)
. (3.62)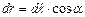 . (3.63)
. (3.63)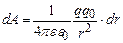 .
. . (3.64)
. (3.64) по замкненій траєкторії точки 1 і 2 будуть співпадати тому
по замкненій траєкторії точки 1 і 2 будуть співпадати тому 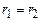 . При цій умові, як випливає із формули (3.64) робота буде дорівнювати нулеві. Тоді формула (3.61) набере вигляду
. При цій умові, як випливає із формули (3.64) робота буде дорівнювати нулеві. Тоді формула (3.61) набере вигляду . (3.65)
. (3.65) . (3.66)
. (3.66) . (3.67)
. (3.67) Потенціалом електричного поля називається скалярна фізична величина рівна потенціальній енергії одиничного позитивного точкового заряду вміщеного в дану точку поля
Потенціалом електричного поля називається скалярна фізична величина рівна потенціальній енергії одиничного позитивного точкового заряду вміщеного в дану точку поля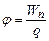 . (3.68)
. (3.68) є вольт. 1В – це потенціал такої точки поля, в якій точковий позитивний заряд величиною 1Кл має потенціальну енергію 1Дж.
є вольт. 1В – це потенціал такої точки поля, в якій точковий позитивний заряд величиною 1Кл має потенціальну енергію 1Дж.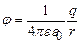 . (3.69)
. (3.69) . (3.70)
. (3.70)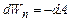 , то
, то . (3.71)
. (3.71)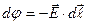 . (3.72)
. (3.72)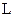 при переміщенні із точки 1 в точку 2
при переміщенні із точки 1 в точку 2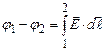 . (3.73)
. (3.73)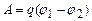 . (3.74)
. (3.74) . Тоді згідно із формулою (3.72) одержимо
. Тоді згідно із формулою (3.72) одержимо , (3.75)
, (3.75) – проекція вектора
– проекція вектора 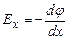 .
. є функцією не лише координати
є функцією не лише координати  і
і  , то в останній формулі слід використати поняття частинної похідної. Тоді формула набере вигляду
, то в останній формулі слід використати поняття частинної похідної. Тоді формула набере вигляду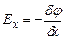 . (3.76)
. (3.76) , (3.77)
, (3.77)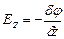 . (3.78)
. (3.78) , (3.79)
, (3.79) – орти.
– орти. . (3.80)
. (3.80)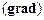
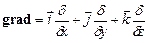 . (3.81)
. (3.81)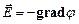 (3.82)
(3.82)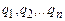 . Тоді його потенціальна енергія рівна сумі потенціальних енергій взаємодії з кожним із зарядів
. Тоді його потенціальна енергія рівна сумі потенціальних енергій взаємодії з кожним із зарядів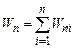 . (3.83)
. (3.83) . (3.84)
. (3.84)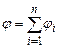 . (3.85)
. (3.85)


