Потік вектора напруженості та індукції електричного поля. Теорема Остроградського-Гауса
Нехай в просторі існує електричне поле, створене деякими електричними зарядами. Розглянемо деяку поверхню з нескінченно малою площею dS (елементарну поверхню) з одиничним вектором нормалі до поверхні
де Подібним чином можна дати визначення елементарного потоку вектора індукції електричного поля, який рівний:
Потік вектора напруженості електричного поля через деяку поверхню S визначається за формулою:
Він пропорційний числу силових ліній, які пронизують цю поверхню. Потік вектора індукції електричного поля через деяку поверхню S рівний:
Розглянемо деякий точковий позитивний заряд
Підставимо (3.15) в (3.14), врахуємо, що кут між векторами
Оскільки для всіх точок сферичної поверхні величина R є постійною то, винісши постійні множники за знак інтегралу, отримаємо:
Але інтеграл по замкнутій поверхні S - це площа сферичної поверхні, яка рівна:
Підставимо вираз (3.17) в (3.16):
Український вчений М.В.Остроградський і німецький вчений К.Гаус довели, що формула (3.18) справедлива для замкненої поверхні довільної форми і довільної кількості електричних зарядів, які знаходяться всередині цієї поверхні. Тому в загальному випадку формулу (3.18) можна представити у вигляді:
Формула (3.19) – це теорема Остроградського-Гауса для напруженості електричного поля:потік вектора напруженості електричного поля через довільну замкнену поверхню рівний алгебраїчній сумі електричних зарядів, охоплених цією поверхнею, поділеній на діелектричну проникність середовища. Помножимо рівняння (3.19) на
Враховуючи (3.7), отримаємо
Формула (3.21) це теорема Остроградського-Гауса для індукції електричного поля: потік вектора індукції електричного поля через довільну замкнену поверхню рівний алгебраїчній сумі електричних зарядів, охоплених цією поверхнею. Розглянемо випадок коли електричні заряди розподілені в просторі неперервно з деякою об’ємною густиною
Визначимо з цієї формули dq:
Проінтегрувавши вираз (3.23) по деякому об’єму V визначимо сумарний електричний заряд який міститься в цьому об’ємі:
З врахуванням формули (3.24) теорему Остроградського-Гауса (3.19) і (3.21) у випадку неперервного просторового розподілу зарядів можна представити у вигляді:
У формулах (3.25) і (3.26) інтегрування здійснюється по всьому об’єму V який обмежений замкненою поверхнею S.
|

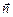 , як зображено на рис.3.3. Нехай в центрі елементарної поверхні напруженість електричного поля рівна
, як зображено на рис.3.3. Нехай в центрі елементарної поверхні напруженість електричного поля рівна  .
. Елементарним потоком вектора напруженості електричного поля називається скалярна величина, рівна скалярному добуткові вектора напруженості електричного поля і одиничного вектора нормалі на площу елементарної поверхні:
Елементарним потоком вектора напруженості електричного поля називається скалярна величина, рівна скалярному добуткові вектора напруженості електричного поля і одиничного вектора нормалі на площу елементарної поверхні: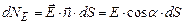 , (3.10)
, (3.10)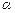 – кут між векторами
– кут між векторами 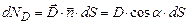 . (3.11)
. (3.11)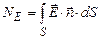 . (3.12)
. (3.12)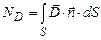 . (3.13)
. (3.13)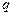 , який помістимо в центрі сферичної поверхні S радіусом R (рис. 3.4). Обчислимо потік вектора напруженості електричного поля через цю замкнену поверхню
, який помістимо в центрі сферичної поверхні S радіусом R (рис. 3.4). Обчислимо потік вектора напруженості електричного поля через цю замкнену поверхню . (3.14)
. (3.14) Напруженість електричного поля точкового заряду в будь якій точці сферичної поверхні рівна
Напруженість електричного поля точкового заряду в будь якій точці сферичної поверхні рівна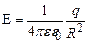 . (3.15)
. (3.15)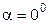 .
.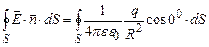 .
.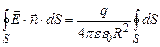 . (3.16)
. (3.16)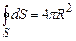 . (3.17)
. (3.17)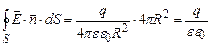 . (3.18)
. (3.18) . (3.19)
. (3.19)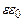 . Враховуючи, що цей множник постійний, внесемо його під знак інтегралу:
. Враховуючи, що цей множник постійний, внесемо його під знак інтегралу: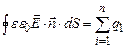 . (3.20)
. (3.20)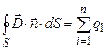 . (3.21)
. (3.21)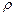 . Об’ємною густиною електричного зарядуназивається фізична величина, рівна електричному зарядові в одиниці об’єму простору:
. Об’ємною густиною електричного зарядуназивається фізична величина, рівна електричному зарядові в одиниці об’єму простору: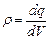 . (3.22)
. (3.22)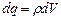 . (3.23)
. (3.23) . (3.24)
. (3.24)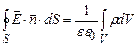 . (3.25)
. (3.25)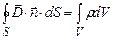 . (3.26)
. (3.26)


