А) Електричне поле рівномірно зарядженої кулі.
Розглянемо кулю радіусом R рівномірно заряджену по об’єму з об’ємною густиною заряду
Для рівномірного розподілу заряду можна вважати що
Оскільки об’єм кулі рівний
то підставивши (3.29) в (3.28) одержимо:
або
В даному випадку
Виходячи з міркувань симетрії випливає, що величина Е за модулем постійна у всіх точках сферичної поверхні S, тому винесемо Е за знак інтегралу:
У формулі (3.34) інтеграл по замкненій поверхні рівний площі сферичної поверхні радіусом r а інтеграл по об’єму V рівний об’єму цієї ж сферичної поверхні, тому
Підставимо вирази (3.30), (3.35) і (3.36) у формулу (3.34):
Отже всередині рівномірно зарядженої по об’єму кулі напруженість електричного поля прямо пропорційна відстані від центру кулі до даної точки. Розглянемо випадок коли
або
Оскільки вектори
Підставимо (3.35) в (3.40):
Із формули (3.41) випливає, що ззовні зарядженої кулі напруженість електричного поля, так само як і для точкового заряду, обернено пропорційна квадратові відстані від центру кулі до даної точки простору. На рис. 3.7 зображено залежність напруженості електричного поля Е від відстані r.
|

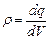 . (3.27)
. (3.27)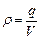 . (3.28)
. (3.28)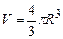 , (3.29)
, (3.29)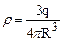 . (3.30)
. (3.30) Виберемо замкнену поверхню S у формі сфери радіусом r, центр якої співпадає з центром зарядженої кулі, як зображено на рис. 3.5. Розглянемо випадок коли
Виберемо замкнену поверхню S у формі сфери радіусом r, центр якої співпадає з центром зарядженої кулі, як зображено на рис. 3.5. Розглянемо випадок коли 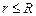 , тобто визначимо напруженість електричного поля всередині зарядженої кулі. Запишемо теорему Остроградського-Гауса для випадку неперервного розподілу електричного заряду.
, тобто визначимо напруженість електричного поля всередині зарядженої кулі. Запишемо теорему Остроградського-Гауса для випадку неперервного розподілу електричного заряду.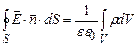 (3.31)
(3.31)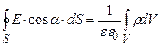 (3.32)
(3.32)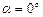 і
і 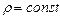 , тому
, тому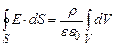 . (3.33)
. (3.33)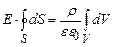 . (3.34)
. (3.34)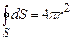 , (3.35)
, (3.35)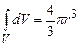 . (3.36)
. (3.36)
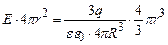
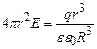
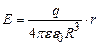 . (3.37)
. (3.37)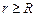 , тобто визначимо напруженість електричного поля ззовні зарядженої кулі (рис. 3.6). Запишемо теорему Остроградського-Гауса.
, тобто визначимо напруженість електричного поля ззовні зарядженої кулі (рис. 3.6). Запишемо теорему Остроградського-Гауса.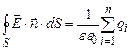 (3.38)
(3.38)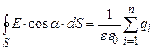 . (3.39)
. (3.39) і
і 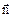 мають однаковий напрямок то
мають однаковий напрямок то 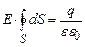 . (3.40)
. (3.40)
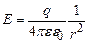 . (3.41)
. (3.41)


