В) Електричне поле нескінченної рівномірно зарядженої площини.Розглянемо нескінченну площину рівномірно заряджену електричним зарядом з поверхневою густиною заряду
Поверхневою густиною електричного заряду називається фізична величина рівна електричному зарядові одиниці площі поверхні по якій розподілений заряд. У випадку рівномірного розподілу електричного заряду q по поверхні S поверхнева густина заряду рівна:
В якості замкненої поверхні виберемо циліндричну поверхню з площею основи Застосуємо теорему Остроградського-Гауса
Інтеграл по замкненій поверхні S запишемо як суму трьох інтегралів. Сумарний заряд, який охоплений поверхнею S рівний зарядові круга площею Sосн ., який вирізує циліндр S на зарядженій площині. Виходячи із формули (3.50), цей заряд рівний
Підставимо (3.52) в (3.51):
Оскільки
Інтеграли по поверхнях основ рівні:
Підставимо (3.54) в (3.53):
Із формули (3.55) випливає, що напруженість електричного поля, створеного нескінченною рівномірно зарядженою площиною не залежить від відстані до площини, тобто є однаковою в усіх точках простору по обидва боки від зарядженої площини. Це електричне поле є однорідним. Його силові лінії перпендикулярні до зарядженої площини.
|
:
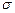. (3.49)
. (3.50)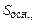
вісь якої перпендикулярна до зарядженої площини, як зображено на рис.3.9.
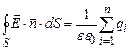. (3.51)
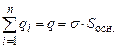(3.52)
і 
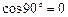, то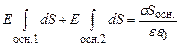
. (3.53)
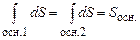(3.54)
. (3.55)
