Б) Електричне поле нескінченої рівномірно зарядженої прямої.
Лінійною густиною електричного заряду називається фізична величина рівна електричному зарядові одиниці довжини лінії вздовж якої він розподілений. У випадку рівномірного розподілу електричного заряду
де В якості замкненої поверхні виберемо циліндричну поверхню радіусом r, висотою
Інтеграл по замкненій поверхні S запишемо як суму трьох інтегралів: по бічній поверхні, по першій і другій основах. Сумарний заряд, який охоплений поверхнею S, рівний зарядові на ділянці прямої довжиною
Підставимо (3.45) в (3.44):
Оскільки
З міркувань симетрії випливає, що модуль Е є однаковим в усіх точках бічної поверхні. Тому винесемо Е за знак інтегралу:
Інтеграл по бічній поверхні рівний площі цієї поверхні:
Підставимо (3.47) у (3.46):
З цієї формули випливає, що напруженість електричного поля, створеного нескінченою рівномірно зарядженою прямою обернено пропорційна до відстані між даною точкою простору і прямою. Ця формула справедлива також для нескінченого прямого рівномірно зарядженого циліндра.
|

 Розглянемо нескінченно довгу пряму, рівномірно заряджену електричним зарядом з лінійною густиною заряду
Розглянемо нескінченно довгу пряму, рівномірно заряджену електричним зарядом з лінійною густиною заряду 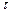 .
. . (3.42)
. (3.42) , (3.43)
, (3.43)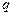 – електричний заряд який розподілений вздовж лінії довжиною
– електричний заряд який розподілений вздовж лінії довжиною  .
.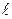 , вісь якої співпадає із зарядженою прямою, як зображено на рис. 3.8. Застосуємо теорему Остроградського-Гауса:
, вісь якої співпадає із зарядженою прямою, як зображено на рис. 3.8. Застосуємо теорему Остроградського-Гауса: . (3.44)
. (3.44)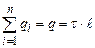 . (3.45)
. (3.45)
 і
і 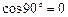 , то одержимо:
, то одержимо: .
.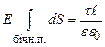 . (3.46)
. (3.46)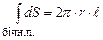 . (3.47)
. (3.47)
 . (3.48)
. (3.48)


