Робота і потужність струму. Закон Джоуля-Ленца
Розглянемо ділянку кола опором R до якої прикладена напруга U і по якій тече струм силою І. Із означення електричної напруги (3.160) визначимо елементарну роботу по переміщенню по колу елементарного заряду dq
Із означення сили струму (3.156) визначимо елементарний заряд
Підставимо вираз (3.212) у формулу (3.211)
Проінтегруємо вираз (3.203) і отримаємо формулу роботи електричного струму
У випадку постійного струму, коли
Потужність рівна роботі виконаній за одиницю часу
Підставимо (3.213) у формулу (3.216). Отримаємо формулу потужності струму
Якщо електричний струм не виконує роботу проти зовнішніх сил і не змінюється внутрішня енергія провідника то, як випливає з першого закону термодинаміки, робота струму рівна кількості теплоти, яка виділяється в провіднику
З закону Ома для ділянки кола випливає
Підставимо (3.219) у формулу (3.218)
У випадку постійного струму формула (3.220) набере вигляду
Формули (3.220) і (3.221) – це закон Джоуля-Ленца в інтегральній формі: кількість теплоти, яка виділяється в провіднику при проходженні електричного струму, прямо пропорційна квадрату сили струму, опору провідника і часу проходження струму Розглянемо циліндричний провідник з площею поперечного перерізу
З формул (3.164) і (3.159) отримаємо
Підставимо (3.223) у формулу (3.222)
де Питомою тепловою потужністю струму називається фізична величина, рівна кількості теплоти, яка виділяється в одиниці об’єму провідника за одиницю часу
Підставимо (3.224) у формулу (3.225) отримаємо
Формула (3.226) – це закон Джоуля-Ленца в диференціальній формі: питома теплова потужність струму прямо пропорційна питомому опору провідника і квадратові густини струму. Використовуючи формули (3.173) вираз (3.226) можне бути представлений у вигляді
Формули (3.227) – це другий варіант закону Джоуля-Ленца в диференціальній формі: питома теплова потужність струму прямо пропорційна питомій електропровідності провідника і квадрату напруженості електричного поля.
|

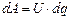 . (3.211)
. (3.211)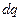
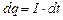 . (3.212)
. (3.212)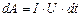 . (3.213)
. (3.213)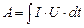 . (3.214)
. (3.214)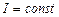 ,
, 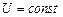 , робота електричного струму визначається за формулою
, робота електричного струму визначається за формулою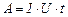 . (3.215)
. (3.215)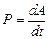 . (3.216)
. (3.216)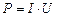 . (3.217)
. (3.217)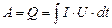 . (3.218)
. (3.218)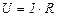 . (3.219)
. (3.219)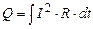 . (3.220)
. (3.220)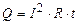 . (3.221)
. (3.221)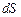 , довжиною
, довжиною 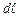 , по якому тече струм силою
, по якому тече струм силою 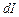 . Тоді за час
. Тоді за час  в ньому виділиться кількість теплоти
в ньому виділиться кількість теплоти 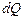 , яка згідно з формулою (3.221) рівна
, яка згідно з формулою (3.221) рівна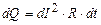 . (3.222)
. (3.222)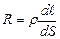 ;
; 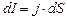 . (3.223)
. (3.223)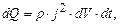 (3.224)
(3.224)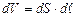 – об’єм провідника.
– об’єм провідника.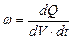 . (3.225)
. (3.225)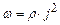 . (3.226)
. (3.226)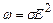 . (3.227)
. (3.227)


