Примеры нахождения асимптот графиков функций.
Пример 1. Найти асимптоты кривой Решение. Найдем горизонтальные асимптоты
Таким образом, кривая имеет единственную горизонтальную асимптоту вида Найдем вертикальные асимптоты
Для определения наклонной асимптоты вида Получим
Пример 2. Найти асимптоты графика функции Решение. Найдем горизонтальные асимптоты по формулам:
Таким образом, кривая имеет единственную горизонтальную асимптоту вида Найдем вертикальные асимптоты. Точки разрыва для данной функции
Таким образом, график имеет две вертикальные асимптоты Для определения наклонной асимптоты вида Получим
Пример 3. Найти асимптоты графика функции Решение. Найдем горизонтальные асимптоты по формулам:
Таким образом, график не имеет горизонтальных асимптот. Найдем вертикальные асимптоты. Точка разрыва для данной функции
Таким образом, график имеет вертикальную асимптоту Для определения наклонной асимптоты вида Получим
то есть график имеет наклонную асимптоту
Пример 4. Найти асимптоты графика функции Решение. Найдем горизонтальные асимптоты по формулам:
Таким образом, график не имеет горизонтальных асимптот. Найдем вертикальные асимптоты. Точка разрыва для данной функции
Таким образом, график имеет левостороннюю (левую) вертикальную асимптоту Для определения наклонной асимптоты вида Получим
Заметим, что при вычислении значения b был использован предел, производный от второго замечательного предела.
|

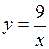
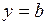 по формулам
по формулам  :
: ,
, 
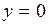 .
. . С этой целью определим точки, вблизи которых функция неограниченно возрастает по абсолютной величине – точки разрыва второго рода. Единственная точка разрыва для данной функции
. С этой целью определим точки, вблизи которых функция неограниченно возрастает по абсолютной величине – точки разрыва второго рода. Единственная точка разрыва для данной функции 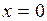 . Определим ее вид:
. Определим ее вид: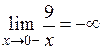 ,
,  . Очевидно, что
. Очевидно, что 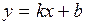 вычислим пределы
вычислим пределы 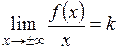 и
и  :
: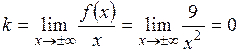 , то есть кривая не имеет наклонной асимптоты.
, то есть кривая не имеет наклонной асимптоты.
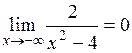 ,
, 
 ,
,  . Исследуем точки разрыва:
. Исследуем точки разрыва: ,
, 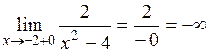 .
. ,
,  .
. .
. , то есть график не имеет наклонной асимптоты.
, то есть график не имеет наклонной асимптоты.
 ,
, 
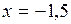 .
.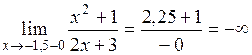 ,
,  .
.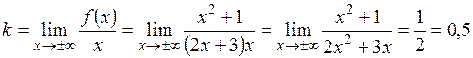 ,
,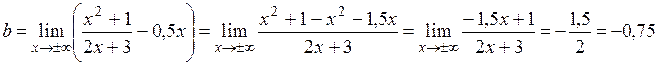 ,
, . Расчеты идентичны при
. Расчеты идентичны при  и
и  , поэтому они объединены.
, поэтому они объединены.
 ,
,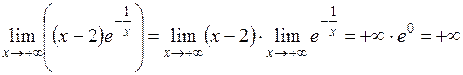
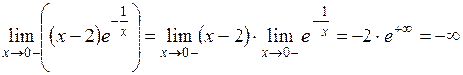 ,
, 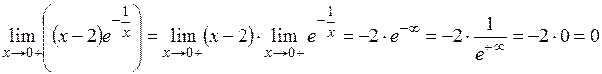 .
.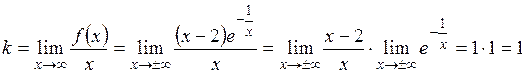 ,
, то есть график имеет наклонную асимптоту
то есть график имеет наклонную асимптоту 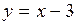 .
.


