I.1.4 Аппроксимация стандартными функциями.
Важная форма обработки численных результатов – их аппроксимация аналитическими функциями, то есть поиск аналитической функции с параметрами, обеспечивающих максимальную близость аналитической функции к исходным численным данным. Origin позволяет проводить аппроксимацию некоторыми стандартными функциями. Для этого следует сделать активным окно, содержащее график. Затем, воспользоваться командой меню Analysis – появляется ниспадающее меню со списком стандартных аппроксимаций. Рассмотрим некоторые варианты из предлагаемых. Fit Liner – аппроксимация прямой линией Fit Polynomial – аппроксимация полиномом, порядок которого может быть от 1 до 9. Порядок полинома (Order) следует вводить вручную. Кроме того, необходимо уточнить число точек, в которых будет вычислен полином (Fit curve # pts), а так же нижнюю (Fit curve Xmin) и верхнюю (Fit curve Xmax) границы аппроксимации. Фактически, использование полинома обеспечивает не только аппроксимацию, но и экстраполяцию (то есть вычисление функции за пределами диапазона определения исходных данных). Границы Xmin и Xmax не обязательно должны совпадать с границами изменения аргумента в исходных данных. Если значения Xmin и/или Xmax выходят за пределы изменений аргумента в исходных данных, то обеспечивается режим экстраполяции. Fit Exponential Decay, First Order – аппроксимация функцией экспоненциального затухания
Все постоянные коэффициенты будут автоматически подобраны так, что бы обеспечить минимум среднеквадратичного отклонения расчетной зависимости от исходных данных. Fit Gaussian – аппроксимация гауссианом В результате аппроксимации на графике отображается аппроксимирующая кривая, которая, по умолчанию, имеет красный цвет. Кроме того, появляется окно Script Window, в котором приведены аппроксимирующая функция, численные значения коэффициентов, среднеквадратичное отклонение и ряд другой полезной информации. В некоторых случаях результаты аппроксимации отображаются в специальном окне непосредственно на графике. Это окно легко перемещается мышкой. Кроме того, оно может быть удалено, если щелкнуть мышкой по этому окну, а затем, нажать клавишу Delete. При использовании интерполяции следует помнить о том, что выбор аналитической функции – это задача для человека, а не для компьютера. Использование аппроксимации корректно в том случае, когда есть физические основания полагать, что экспериментальная зависимость описывается той или иной аналитической функцией. Особую аккуратность следует соблюдать при использовании полиномиальной аппроксимации и, особенно, в трактовке полученных численных значений постоянных коэффициентов. Так, например, увеличение степени полинома может практически не изменить вид функции, но привести с существенным изменениям коэффициентов при младших степенях независимой переменной. Поэтому, обсуждение физического смысла постоянных коэффициентов корректно лишь в тех случаях, когда есть физические основания для ограничения степени аппроксимирующего полинома.
|

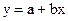 . Коэффициенты a и b будут автоматически подобраны так, что бы обеспечить минимум среднеквадратичного отклонения [6,7] расчетной линии от исходных данных.
. Коэффициенты a и b будут автоматически подобраны так, что бы обеспечить минимум среднеквадратичного отклонения [6,7] расчетной линии от исходных данных.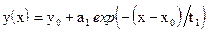 .
.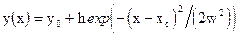 .
.


