Стационарное состояние точечной системы является устойчивым фокусом(для модели с двумя переменными); 2) имеется интервал значений волновых чисел (kmin, kmax) при которых дисперсионное уравнение имеет два действительных корня с разными Знаками. Если эти условия выполняются, то зависимость Re p от k имеет вид, представленный на рис. 2.
Анализ дисперсионного уравнения показывает, что устойчивое в отсутствие Диффузии однородное состояние системы может стать неустойчивым. Таким образом, А.Тьюринг, увидел в уравнениях (1) принципиальную Возможность описания морфогенеза.
|
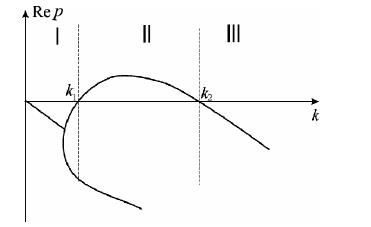Рис.2.
