Матрицы. Операции над матрицами: сложение , умножение матрицы на число, умножение матриц
Матрицей m × n называется прямоугольный массив чисел, состоящий из m строк и n столбцов. Количество строк и столбцов определяет размер матрицы. Отдельный элемент матрицы идентифицируется путем указания его строки и столбца в состоящем из двух элементов спсике индексов; первый индекс определяет строку, а второй — столбец. Ниже в качестве примера приведены матрицы M размером 3 × 3, В размером 2 × 4 и С размером 3 × 2:
Сложение матриц Определение 14.2 Суммой матриц Другими словами, при сложении матриц складываются элементы, стоящие на одинаковых местах. Например,
Умножение матрицы на число
Определение 14.3 Произведением матрицы Другими словами, при умножении матрицы на число все ее элементы умножаются на это число. Например, Операцию вычитания матриц можно определить следующим способом:
что соответствует вычитанию элементов, стоящих на одинаковых местах.
Умножение матриц Чтобы получить произведение матриц AB необходимо чтобы количество столбцов матрицы A было равно количеству строк матрицы B. Если условие выполняется, произведение матриц определено. Рассмотрим представленные ниже матрицы A и B, с размерностью 2 × 3 и 3 × 3 соответственно:
Если A — это матрица m × n, а B — матрица n × p, то их произведением будет матрица C, размером m × p, в которой элемент cij находится как скалярное произведение i -го вектора-строки матрицы A и j -го вектора-столбца матрицы B:
В этой формуле a i обозначает i -ый вектор-строку в матрице A, а b j — j -ый вектор-столбец матрицы B. Давайте для примера вычислим произведение:
Произведение определено, поскольку количество столбцов матрицы A равно количеству строк матрицы B. Кроме того, обратите внимание, что размер полученной в результате матрицы — 2 × 2. Согласно формуле (4) получаем:
В качестве упражнения проверьте, что в данном случае AB ≠ BA.
. Свойства этих операций Легко проверить, что операции сложения матриц и умножения матрицы на число, называемые линейными операциями, обладают следующими свойствами:
Здесь
|


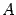 и
и  размеров
размеров 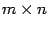 является матрица
является матрица  таких же размеров, у которой
таких же размеров, у которой  ,
,  ,
,  .
.
 называется матрица
называется матрица  ,
, 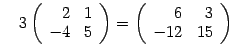 .
.




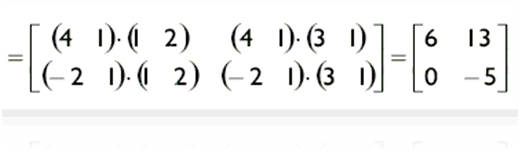


 ;
; 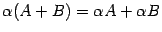
 ;
; 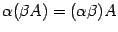 ;
; 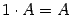 .
. 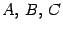 -- матрицы,
-- матрицы,  -- числа, 0 -- нулевая матрица.
-- числа, 0 -- нулевая матрица.


