Метод Крамера
Данный метод также применим только в случае систем линейных уравнений, где число переменных совпадает с числом уравнений. Кроме того, необходимо ввести ограничения на коэффициенты системы. Необходимо, чтобы все уравнения были линейно независимы, т.е. ни одно уравнение не являлось бы линейной комбинацией остальных. Для этого необходимо, чтобы определитель матрицы системы не равнялся 0. det A ¹ 0; в случае, если определитель матрицы системы не равен нулю, имеет единственное решение и это решение находится по формулам:
xi = Di/D, где
D = det A, а Di – определитель матрицы, получаемой из матрицы системы заменой столбца i столбцом свободных членов bi.
Di =
Метод Гауса
Рассмотрим систему линейных уравнений:
Разделим обе части 1–го уравнения на a11 ¹ 0, затем: 1) умножим на а21 и вычтем из второго уравнения 2) умножим на а31 и вычтем из третьего уравнения и т.д.
Получим:
где d1j = a1j/a11, j = 2, 3, …, n+1.
dij = aij – ai1d1j i = 2, 3, …, n; j = 2, 3, …, n+1. Далее повторяем эти же действия для второго уравнения системы, потом – для третьего и т.д. Пример. Решить систему линейных уравнений методом Гаусса.
Составим расширенную матрицу системы.
Составим расширенную матрицу системы. А* =
Таким образом, исходная система может быть представлена в виде:
A =
x1 = D1/detA; x2 = D2/detA; x3 = D3/detA;
Пример. Найти решение системы уравнений:
D = D1 =
x1 = D1/D = 1; D2 =
x2 = D2/D = 2; D3 = x3 = D3/D = 3.
|



 ,
,
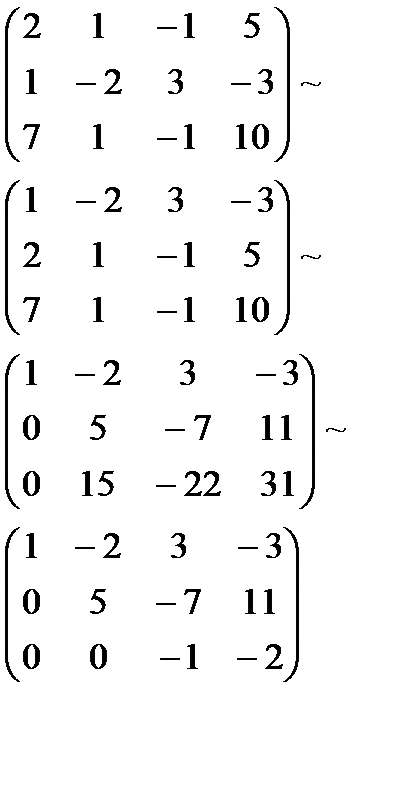
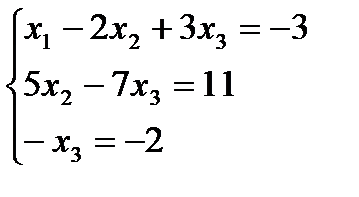 , откуда получаем: x3 = 2; x2 = 5; x1 = 1.
, откуда получаем: x3 = 2; x2 = 5; x1 = 1.
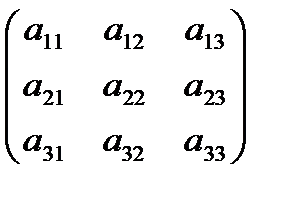 ; D1=
; D1= 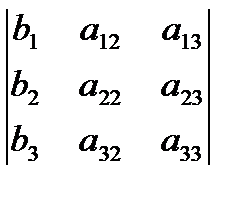 ; D2=
; D2= 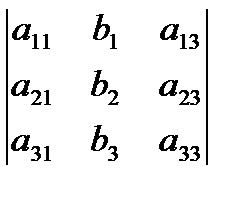 ; D3=
; D3= 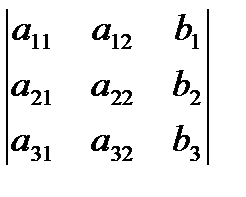 ;
;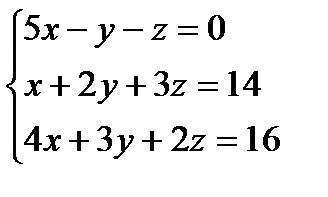
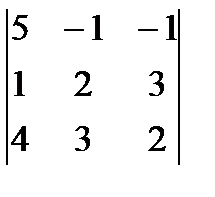 = 5(4 – 9) + (2 – 12) – (3 – 8) = -25 – 10 + 5 = -30;
= 5(4 – 9) + (2 – 12) – (3 – 8) = -25 – 10 + 5 = -30;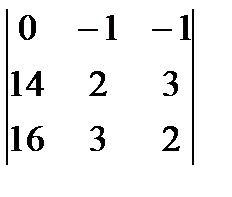 = (28 – 48) – (42 – 32) = -20 – 10 = -30.
= (28 – 48) – (42 – 32) = -20 – 10 = -30. = 5(28 – 48) – (16 – 56) = -100 + 40 = -60.
= 5(28 – 48) – (16 – 56) = -100 + 40 = -60.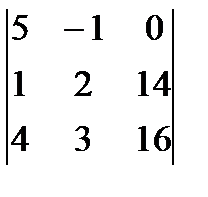 = 5(32 – 42) + (16 – 56) = -50 – 40 = -90.
= 5(32 – 42) + (16 – 56) = -50 – 40 = -90.


