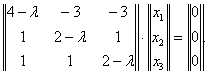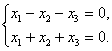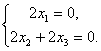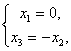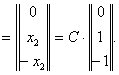Найти собственные значения и собственные векторы матрицы
Решение
Или
Раскроем скобки и приведём подобные слагаемые
или
Отсюда
или
Вынесем общий множитель за скобки. Тогда получим уравнение
Произведение равно нулю, когда один из сомножителей равен нулю. Получаем совокупность уравнений
Второе уравнение совокупности - квадратное уравнение с отрицательным дискриминантом
Следовательно оно не имеет действительных корней. Поэтому характеристическое уравнение имеет только один действительный корень
Расписывая по компонентам и подставляя
Второе и третье уравнения одинаковые. Поэтому систему можно переписать в виде:
Сложим оба уранения, а затем из второго вычтем первое. Получим
Отсюда
и мы имеем собственный вектор x=
|
.
.
.
.
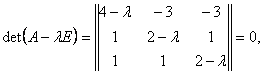
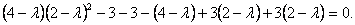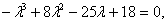
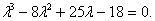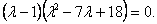
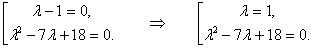
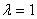, а матрица только одно собственное значение 
