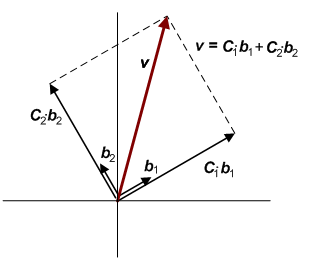
Разложение вектора по орторнормированному базису
Ортонормированный базис в двумерном пространстве – пара взаимно перпендикулярных единичных векторов, которые в совокупности с парой параметров однозначно выражают вектор в двумерном пространстве. Вектор v может быть разложен по ортонормированному базису { b 1, b 2} следующим образом v = C 1· b 1 + C 2· b 2 (1) Коэффициенты C 1 и C 2 выражают величину вектора v в направлениях b 1 и b 2. Векторы C 1· b 1 и C 2· b 2 называются проекциями вектора v.
Рисунок 1 Выведем коэффициенты C 1 и C 2. Найдем скалярное произведение левой и правой частей равенства (1) и вектора b 1. < v, b 1> = < C 1· b 1 + C 2· b 2, b 1> = < C 1· b 1, b 1> + < C 2· b 2, b 1> = C 1< b 1, b 1> + C 2< b 2, b 1> Так как { b 1, b 2} – ортонормированный базис, скалярное произведение < b 1, b 1> равно 1 (квадрат нормы вектора b 1), а скалярное произведение < b 2, b 1> равно 0 (так как векторы b 2, b 1 перпендикулярны). Таким образом C 1 = < v, b 1> (2) Аналогичным образом найдем скалярное произведение левой и правой частей равенства (1) и вектора b 2. < v, b 2> = < C 1· b 1 + C 2· b 2, b 2 > = < C 1· b 1, b 2> + < C 2· b 2, b 2> = C 1< b 1, b 2> + C 2< b 2, b 2> Согласно свойствам ортонормированного базиса < b 1, b 2> = 0, < b 2, b 2> = || b 1||2 = 1, следовательно C 2 = < v, b 2> (3)
Рассмотрим простейший пример. Выясним, образуют ли векторы b 1 = (1, 0) и b 2 = (0, 1) ортонормированный базис. Для начала посчитаем нормы векторов b 1 и b 2 и убедимся в том, что они равны 1, т.е. векторы являются единичными. || b 1|| = || b 2|| = Теперь посчитаем скалярное произведение векторов b 1 и b 2 и убедимся, что оно равно 0. < b 1, b 2> = 1·0 + 0·1 = 0 Так как векторы b 1 и b 2 являются единичными и ортогональны (их скалярное произведение равно нулю) они образуют ортонормированный базис. Теперь разложим по базису { b 1, b 2} вектор v = (2, 3) C 1 = < v, b 1> = 2·1 + 3·0 = 2 C 2 = < v, b 2> = 2·0 + 3·1 = 3 v = 2· b 1 + 3· b 2
|

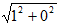 = 1
= 1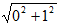 = 1
= 1


