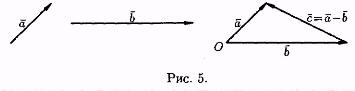Векторная алгебра
Векторы. Основные понятия Основные понятия Величины, которые полностью определяются своим численным значением, называются скалярными. Примерами скалярных величин являются: площадь, длина, объем, температура, работа, масса. Другие величины, например сила, скорость, ускорение, определяются не только своим числовым значением, но и направлением. Такие величины называют векторными. Векторная величина геометрически изображается с помощью вектора. Вектор - это направленный прямолинейный отрезок, т. е. отрезок, имеющий определенную длину и определенное направление. Если А — начало вектора, а В - его конец, то вектор обозначается символом АВ или а. Вектор ВА (у него начало в точке В, а конец в точке A) называется противоположным вектору АВ. Вектор, противоположный вектору а, обозначается -а. Длиной или модулем вектора АВ называется длина отрезка и обозначается |АВ|. Вектор, длина которого равна нулю, называется нулевым вектором и обозначается 0. Нулевой вектор направления не имеет. Вектор, длина которого равна единице, называется единичным вектором и обозначается через e. Единичный вектор, направление которого совпадает с направлением вектора a, называется ортом вектора a и обо значается a °. Векторы а и b называются коллинеарными, если они лежат на одной прямой или на параллельных прямых; записывают a ||b. Коллинеарные векторы могут быть направлены одинаково или противоположно. Нулевой вектор считается коллинеарным любому вектору. Два вектор а и b называются равными (а = b), если они коллинеарны, одинаково направлены и имеют одинаковые длины.
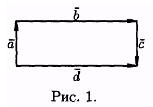
Из определения равенства векторов следует, что вектор можно переносить параллельно самому себе, а начало вектора помещать в любую точку О пространства. На рисунке 1 векторы образуют прямоугольник. Справедливо равенство b =d, но а¹ с. Векторы а и с — противоположные, а =-с. Равные векторы называют также свободными. Три вектора в пространстве называются компланарными, если они лежат в одной плоскости или в параллельных плоскостях. Если среди трех векторов хотя бы один нулевой или два любые коллинеарны, то такие векторы компланарны . Линейные операции над векторами Под линейными операциями над векторами понимают операции сложения и вычитания векторов, а также умножение вектора на число. Пусть а и b — два произвольных вектора. Возьмем произвольную точку О и построим вектор ОА=а. От точки А отложим вектор АВ = b. Вектор ОВ, соединяющий начало первого вектора с концом второго, называется суммой векторов а и b: О B=а+b (см. рис. 2)
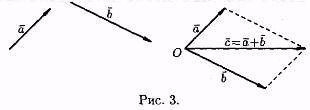
Это правило сложения векторов называют правилом треугольника. Сумму двух векторов можно построить также по правилу параллелoграмма (см. рис. 3).
На рисунке 4 показано сложение трех векторов а, b и с.
Под разностью векторов а и b понимается вектор с=а-b такой, что b+с=а (см. рис. 5).
Отметим, что в параллелограмме, построенном на векторах а и b одна направленная диагональ является суммой векторов а и b, адругая — разностью (см. рис. 6).
Можно вычитать векторы по правилу: а - b = а + (-b), т. е. вычитание векторов заменить сложением вектора а с вектором, противоположным вектору b. Произведением вектора а на скаляр (число) λ называется вектор λ*а (или а*λ), который имеет длину |λ|*|а|, коллинеарен вектору а, имеет направление вектора а, если λ>0 и противоположное направление, если λ<0. Из определения произведения вектора на число следуют свойства этого произведения: 1) если b=λ * а, то b|| а. Наоборот, если b || а, ( а¹0), то при некотором λ верно равенство b = λа; 2) всегда а =|а | • а -о, т. е. каждый вектор равен произведению его мо дуля на орт. Линейные операции над векторами обладают следующими свойствами: 1. а+b=b+а Эти свойства позволяют проводить преобразования в линейных операциях с вектором так, как это делается в обычной алгебре: слагаемые менять местами, вводить скобки, группировать, выносить за скобки как скалярные, так и векторные общие множители.
|

 .
.